Advertisements
Advertisements
प्रश्न
A car has two wipers that do not overlap. Each wiper has a blade of length 21 cm sweeping through an angle of 120°. Find the total area cleaned at each sweep of the blades. `("Take" π =22/7)`
उत्तर
Radius = r = 21 cm
sweeping angle = 120°
Total area cleaned by two wipers `= 2 xx "area cleaned by one wiper"`
Total area cleaned by two wipers `= 2 xx "area of sector with" 120^@`
`= 2 xx theta /360 xx pi"r"^2`
On substituting the values `= 2 xx 120/360 xx 22/7 xx (21)^2`
`= 2 xx 120/360 xx 22/7 xx 441`
`= (2 xx 22 xx 147)/7`
`= 6468/7 = 924`
Therefore, the area cleaned by both wipers is 924 cm2.
APPEARS IN
संबंधित प्रश्न
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:
(i) The length of the arc
(ii) Area of the sector formed by the arc
(iii) Area of the segment forced by the corresponding chord
[use Π = 22/7]
The area of sector of circle of radius 5cm is 5𝜋 cm2. Find the angle contained by the sector.
A chord of a circle subtends an angle 𝜃 at the centre of circle. The area of the minor segment cut off by the chord is one eighth of the area of circle. Prove that 8 sin`theta/2 "cos"theta/2+pi =(pitheta)/45`

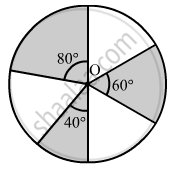
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
If angle of sector is 60°, radius is 3.5 cm then length of the arc is ____________.
The areas of two sectors of two different circles with equal corresponding arc lengths are equal. Is this statement true? Why?
The number of revolutions made by a circular wheel of radius 0.25 m in rolling a distance of 11 km is ______.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
