Advertisements
Advertisements
प्रश्न
In figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.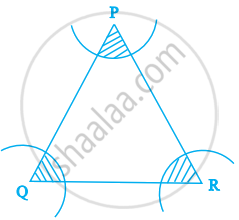
उत्तर
Given that, radii of each arc (r) = 14 cm
Now, area of the sector with central angle P
= `(∠"P")/360^circ xx π"r"^2`
= `(∠"P")/360^circ xx π xx (14)^2 "cm"^2`
Area of the sector with central angle Q
= `(∠"Q")/360^circ xx π"r"^2`
= `(∠"Q")/360^circ xx π xx (14)^2 "cm"^2`
And area of the sector with central angle R
= `(∠"R")/360^circ xx π"r"^2`
= `(∠"R")/360^circ xx π xx (14)^2 "cm"^2`
Therefore, sum of the areas of three sectors
= `(∠"P")/360^circ xx π xx (14)^2 + (∠"Q")/360^circ xx π xx (14)^2 + (∠"R")/360^circ xx π xx (14)^2`
= `π/360^circ xx (14)^2 xx [∠"P" + ∠"Q" + ∠"R"]`
= `π/360^circ xx 196 xx 180^circ` ...[Since, sum of all interior angles in any triangle is 180°]
= 98π
= `98 xx 22/7`
= 14 × 22
= 308
Hence, the required area of the shaded region is 308 cm2.
APPEARS IN
संबंधित प्रश्न
Find the area of the sector whose arc length and radius are 14 cm and 6 cm respectively.
A sector of a circle of radius 8cm contains the angle of 135°. Find the area of sector.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 𝜃. The area of the minor segment cutoff by AC is equal to twice the area of sector BOC.Prove that `"sin"theta/2. "cos"theta/2= pi (1/2−theta/120^@)`

In the given figure, if O is the centre of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of shaded region is 114 cm2 , find the radius of the circle. \[\pi\] = 3.14)

Area of a sector of central angle 200° of a circle is 770 cm2. Find the length of the corresponding arc of this sector.
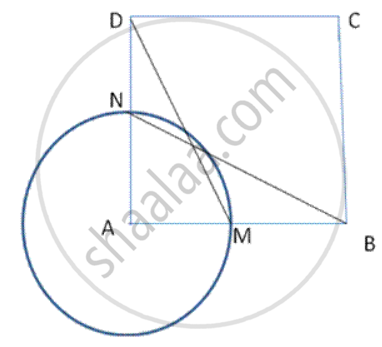
In following fig., ABCD is a square. A cirde is drawn with centre A so that it cuts AB and AD at Mand N respectively. Prove that Δ DAM ≅ Δ .BAN.
A piece of wire 20 cm long is bent into the form of an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively 120° and 40°. Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe?
Radius of a circle is 10 cm. Measure of an arc of the circle is 54°. Find the area of the sector associated with the arc. (π = 3.14)
Given: The radius of a circle (r) = `square`
Measure of an arc of the circle (θ) = `square`
Area of the sector = `θ/360^circ xx square`
= `square/360^circ xx square xx square xx square`
= `square xx square xx square`
= 47.10 cm2
