Advertisements
Advertisements
प्रश्न
In the given figure, arcs have been drawn of radius 7 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
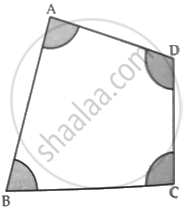
उत्तर
Let the measure of ∠A, ∠B, ∠C and ∠D be θ1, θ2, θ3 and θ4 respectively
Required area = Area of sector with centre A + Area of sector with centre B + Area of sector with centre C + Area of sector with centre D
= `θ_1/360 xx π xx 7^2 + θ_2/360 xx π xx 7^2 + θ_3/360 xx π xx 7^2 + θ_4/360 xx π xx 7^2`
= `((π_1 + π_2 + π_3 + π_4))/360 xx pi xx 7^2`
= `((360))/360 xx 22/7 xx 7 xx 7` ......(By angle sum property of a triangle)
= 154 cm2
APPEARS IN
संबंधित प्रश्न
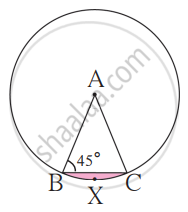
In the given figure, A is the center of the circle. ∠ABC = 45° and AC = 7√2 cm. Find the area of segment BXC.
In the given figure, if O is the center of the circle, PQ is a chord. \[\angle\] POQ = 90°, area of the shaded region is 114 cm2, find the radius of the circle. \[\pi\] = 3.14)

The radius of a circle is 17.5 cm. Find the area of the sector enclosed by two radii and an arc 44 cm in length.
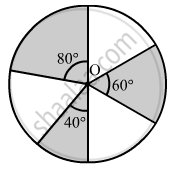
In the given figure, three sectors of a circle of radius 7 cm, making angles of 60°, 80° and 40° at the centre are shaded. Find the area of the shaded region.
The diameter of a sphere is 6 cm, Find the total surface area of the sphere. (π = 3.14)
The area of the largest square that can be inscribed in a circle of radius 12 cm is ____________.
If `theta` is the angle in degrees of a sector of a circle of radius V, then area of the sector is ____________.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm.
With vertices A, B and C of ΔABC as centres, arcs are drawn with radii 14 cm and the three portions of the triangle so obtained are removed. Find the total area removed from the triangle.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the segment formed by the corresponding chord. (Use π = `22/7`)
