Advertisements
Advertisements
Question
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
Solution
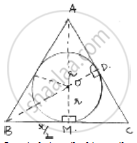
Let circle inscribed in equilateral triangle
Be with centre O and radius ‘r’
Area of circle = 𝜋r2
ut given that area = 154 cm2.
𝜋r2 = 154
`22/7xxr^2 = 154`
𝑟2 = 7 × 7
r = 7cms
Radius of circle = 7cms
From fig. at point M, BC side is tangent at point M, BM ⊥ OM. In equilateral triangle, the perpendicular from vertex divides the side into two halves
BM = `1/2 BC = 1/2 (side =x) = x/2`
ΔBMO is right triangle, by Pythagoras theorem
`OB^2= BM^2+MO^2`
`OB=sqrt(r^2+(x^2/4 ))=sqrt(49+x^2/4)`OD=r
Altitude BD`=sqrt(3)/2(side)=sqrt(3)/2x=OB+OD`
BD – OD = OB
⇒`sqrt(3)/2x-r=sqrt(49+x^2/4`
⇒`sqrt(3)/2x-7=sqrt(49+x^2/4`
⇒`(sqrt(3)/2x-7)^2=(sqrt(x^2/4+49))^2`
⇒`3/4x^2-7sqrt(3x)+49=x^2/4+49`
⇒`x/2=7sqrt(3)⇒x=14sqrt(3)cm`
Perimeter =`3x=3xx14sqrt(3)`
`=42sqrt(3)cms`
APPEARS IN
RELATED QUESTIONS
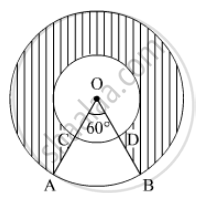
In Figure , two concentric circles with centre O, have radii 21cm and 42 cm. If ∠ AOB = 60°, find the area of the shaded region. [use π=22/7]
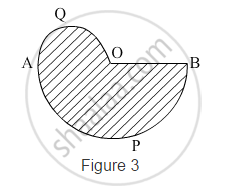
In Fig. 3, APB and AQO are semicircles, and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region [Use `pi=22/7`]
A bicycle whell makes 5000 revolutions in moving 11 km. Find the diameter of the wheel
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
The length of a chain used as the boundary of a semicircular park is 108 m. Find the area of the park.
The circumference of a garden roller is 280 cm. How many revolutions does it make in moving 490 meters?
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 8 cm , diameter = 12 cm
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
Construct an angle PQR = 45°. Mark a point S on QR such that QS = 4.5 cm. Construct a circle to touch PQ at Q and also to pass through S.
Is it true that the distance travelled by a circular wheel of diameter d cm in one revolution is 2 π d cm? Why?
