Advertisements
Advertisements
प्रश्न
The area of circle, inscribed in equilateral triangle is 154 cms2. Find the perimeter of
triangle.
उत्तर
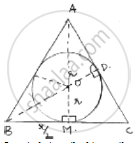
Let circle inscribed in equilateral triangle
Be with centre O and radius ‘r’
Area of circle = 𝜋r2
ut given that area = 154 cm2.
𝜋r2 = 154
`22/7xxr^2 = 154`
𝑟2 = 7 × 7
r = 7cms
Radius of circle = 7cms
From fig. at point M, BC side is tangent at point M, BM ⊥ OM. In equilateral triangle, the perpendicular from vertex divides the side into two halves
BM = `1/2 BC = 1/2 (side =x) = x/2`
ΔBMO is right triangle, by Pythagoras theorem
`OB^2= BM^2+MO^2`
`OB=sqrt(r^2+(x^2/4 ))=sqrt(49+x^2/4)`OD=r
Altitude BD`=sqrt(3)/2(side)=sqrt(3)/2x=OB+OD`
BD – OD = OB
⇒`sqrt(3)/2x-r=sqrt(49+x^2/4`
⇒`sqrt(3)/2x-7=sqrt(49+x^2/4`
⇒`(sqrt(3)/2x-7)^2=(sqrt(x^2/4+49))^2`
⇒`3/4x^2-7sqrt(3x)+49=x^2/4+49`
⇒`x/2=7sqrt(3)⇒x=14sqrt(3)cm`
Perimeter =`3x=3xx14sqrt(3)`
`=42sqrt(3)cms`
APPEARS IN
संबंधित प्रश्न
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
A conical tent requires 264 m2 of canvas. If the slant height is 12 m, find the vertical height of the cone.
A cart wheel makes 9 revolutions per second. If the diameter of the wheel is 42 cm, find its speed in km/hr.
Find the volume and the surface area of the spheres in the following :
Diameter= 6.3 cm
A solid sphere metal is cut through its centre into 2 equal parts. If the diameter of the sphere is 3`1/3` cm , find the total surface of each part, correct to two decimal places.
The shaded portion of the figure, given alongside, shows two concentric circles. If the circumference of the two circles is 396 cm and 374 cm, find the area of the shaded portion.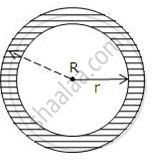
Ratio of the circumference of a circle to its diameter is denoted by symbol ______.
