Advertisements
Advertisements
Question
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
Solution
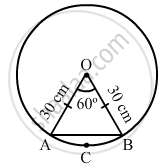
Let the chord be AB. The ends of the chord are connected to the centre of the circle O to give the triangle OAB.
OAB is an isosceles triangle. The angle at the centre is 60°
Area of the triangle `=1/2(30)^2 sin 60^circ = 450xxsqrt(3)/2 = 389.25 "cm"^2`
Area of the sector OACBO` =60/360xxpixx30xx30 = 150pi = 471 "cm"^2`
Area of the minor segment = Area of the sector - Area of the minor segment
= (π × 30 × 30) - 81.29
= 2744.71 cm2
APPEARS IN
RELATED QUESTIONS
The inner circumference of a circular track is 220 m. The track is 7m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of j – 2 per metre. (Use π = 22/7)
The area of rhombus is `480cm^2` , and one of its diagonal measures 48 cm. Find
(i) the length of the other diagonal,
(ii) the length of each of the sides
(iii) its perimeter
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
The perimeter of a sector of a circle of radius 5.6 cm is 27.2 cm. Find the area of the sector.
In the given figure, the area of the shaded portion is 770 cm2. If the circumference of the outer circle is 132 cm, find the width of the shaded portion.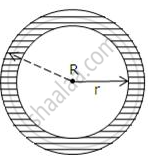
Find the circumference of the circle whose area is 25times the area of the circle with radius 7cm.
The radius of the wheel of a bus is 0.7 m. How many rotations will a wheel complete while traveling a distance of 22 km?
Find the circumference of the circles whose radii are given below.
91 mm
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm.
Circumference ‘C’ of a circle can be found by multiplying diameter ‘d’ with ______.
