Advertisements
Advertisements
Question
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
Solution
Let the length of the major arc be x cm
Radius of the circle = 10.5 cm
∴ Length of the minor arc`=x/5 "cm"`
Circumference `= (x + x/5) = "6x"/5 "cm"`
Using the given data, we get :
`(6x)/5 = 2xx22/7xx21/2`
`=>(6x)/5 = 66`
Or.
x = 55
∴ Area of the sector corresponding to the major arc `= (1/2xx55xx21/2) = 288.75 "cm"^2`
APPEARS IN
RELATED QUESTIONS
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
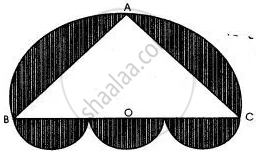
A doorway is decorated as shown in the figure. There are four semi-circles. BC, the diameter of the larger semi-circle is of length 84 cm. Centres of the three equal semicircles lie on BC. ABC is an isosceles triangle with AB = AC. If BO = OC, find the area of the shaded region. (Take `pi = 22/7`)
Find the angle subtended at the centre of circle of radius 5cm by an arc of length `((5pi)/3)` cm
The hypotenuse of a right-angled triangle is 65 cm and its base is 60 cm. Find the length of perpendicular and the area of the triangle.
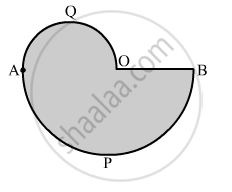
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
A wire when bent in the form of an equilateral triangle encloses an area of `121sqrt(3) "cm"^2`. The same wire is bent to form a circle. Find the area enclosed by the circle.
The sum of the radii of two circles is 7 cm, and the difference of their circumferences is 8 cm. Find the circumference of the circles.
A wire is in the form of a circle of radius 42 cm. It is bent into a square.
Determine the side of the square and compare the area of the regions enclosed in two cases.
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
Diameters of different circles are given below. Find their circumference (Take π = `22/7`)
d = 56 m
