Advertisements
Advertisements
प्रश्न
The perimeter of a rhombus is 60 cm. If one of its diagonal us 18 cm long, find
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
उत्तर
Perimeter of a rhombus = 4a (Here, a is the side of the rhombus)
⇒ `60=4a `
⇒ `a=15`
(i) Given:
One of the diagonals is 18 cm long
`d_1= 18cm`
Thus, we have:
Side= `1/2sqrt(d_1^2+d_2^2)`
⇒ `15=1/2sqrt(18^2+d_2^2)`
⇒`30=sqrt(18^2+d_2^2)`
Squaring both sides, we get:
⇒`900=18^2+d_2^2`
⇒`900=324+d_2^2`
⇒`d_2^2=576`
⇒`d_2^2=24cm`
(ii) Area of the rhombus=`1/2d_1xxd_2`
=`1/2xx18xx24`
=`216 cm^2`
APPEARS IN
संबंधित प्रश्न
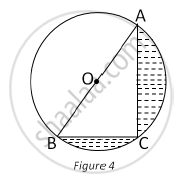
In Fig. 4, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Find in terms of x the length of the arc that subtends an angle of 30°, at the centre of circle of radius 4 cm.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
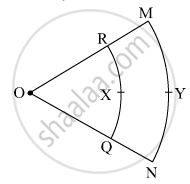
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
Each side of a square is 44 cm. Find its perimeter. If this perimeter is equal to the circumference of a circle, find the radius of the circle.
Find the area and perimeter of the following semicircles: Diameter = 5.6cm
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
The area of a semicircle of radius 4r is ______.
