Advertisements
Advertisements
प्रश्न
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
उत्तर
Radius of sphere = 10 cm
Volume of sphere = `4/3pir^3`
= `4/3 xx 22/7 xx 10 xx 10 xx 10 "cm"^3`
= 4190.476 cm3
Therefore , Volume of water = 4190.476 cm3
Radius of base of cylinder = 20 cm
Let h be the height of the water
⇒ `pir^2h = 4190.476`
⇒ `22/7 xx 20 xx 20 xx h = 4190.476`
⇒ `1257.143 h = 4190.476`
⇒ h = 3.33 cm
lncrease in water level = 3.33 cm
APPEARS IN
संबंधित प्रश्न
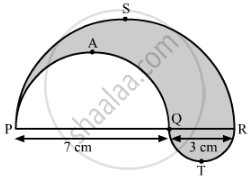
In PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π=3.14]
A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
Find the area of the sector of a circle whose radius is 14 cm and angle of sector is 45º
A car travels 1 km distance in which each wheel makes 450 complete revolutions. Find the radius of wheel.
Find the diameter of the circle whose area is equal to the sum of the areas of two circles having radii 4 cm and 3 cm.
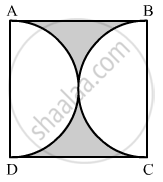
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
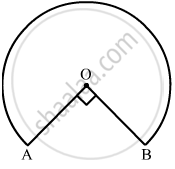
In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and ∠AOB = 90°. If AO = OB = 42 cm,· then find the perimeter of the top of the table.
A square ABCD is inscribed in a circle of radius r. Find the area of the square.
Find the area enclosed between two concentric circles, if their radii are 6 cm and 13 cm respectively.
A conical tent with a capacity of 600 m3 stands on a circular base of area 160 m2 Find in m2 the area of the canvas.
Find the diameter of the sphere for the following :
Volume = `72pi "cm"^3`
The circumference of a circular field is 308 m. Find is:
(i) Radius
(ii) Area.
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
The diameter of a circular field is 56 m. Find its circumference and cost of fencing it at the rate of ₹80 per m. (Take π =`22/7`)
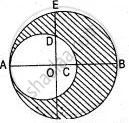
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
Find the perimeter of the given shape (Take π = `22/7`).
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
Ratio of circumference of a circle to its radius is always 2π:I.
