Advertisements
Advertisements
प्रश्न
A cylindrical bucket, whose base radius is 20 cm, is filled with water to a height of 25 cm. A heavy iron spherical ball of radius 10 cm is dropped to submerge completely in water in the bucket. Find the increase in the level of water.
उत्तर
Radius of sphere = 10 cm
Volume of sphere = `4/3pir^3`
= `4/3 xx 22/7 xx 10 xx 10 xx 10 "cm"^3`
= 4190.476 cm3
Therefore , Volume of water = 4190.476 cm3
Radius of base of cylinder = 20 cm
Let h be the height of the water
⇒ `pir^2h = 4190.476`
⇒ `22/7 xx 20 xx 20 xx h = 4190.476`
⇒ `1257.143 h = 4190.476`
⇒ h = 3.33 cm
lncrease in water level = 3.33 cm
APPEARS IN
संबंधित प्रश्न
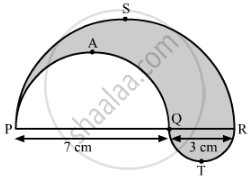
In PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π=3.14]
A sheet of paper is in the form of rectangle ABCD in which AB = 40cm and AD = 28 cm. A semicircular portion with BC as diameter is cut off. Find the area of remaining paper.
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
Choose the correct alternative answer for the following question.
The curved surface area of a cylinder is 440 cm 2 and its radius is 5 cm. Find its height.
The difference between the circumference and radius of a circle is 37cm. Using `pi = 22/7` , find the circumference of the circle.
The side of a square is 10 cm. Find the area of the circumscribed circle. [π = 3.14]
Find the area of the circle if its circumfence is 88 cm.
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
A conical tent requires 264 m2 of canvas. If the slant height is 12 m, find the vertical height of the cone.
A lawn is in the shape of a semi-circle of diameter 42 m. The lawn is surrounded by a flower bed of width 7 m all around. Find the area of the flower bed in m2 .
A cart wheel makes 9 revolutions per second. If the diameter of the wheel is 42 cm, find its speed in km/hr.
A cylindrical beaker of 7 cm diameter is partly filled with water. Determine the number of spherical marbles of diameter 1.4 cm that are to be submerged in it to raise the water level by 5.6 cm
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width of 3.5 m. Find the area of the path.
The inner circumference of a circular track is 264 m and the width of the track is 7 m. Find:
(i) the radius of the inner track.
(ii) the radius of the outer circumference.
(iii) the length of the outer circumference.
(iv) the cost of fencing the outer circumference at the rate of ₹50 per m.
Find the area and perimeter of the circles with following: Radius = 10.5cm
The circumference of a circle exceeds its diameter by 450 cm. Find the area of the circle.
Formula used to find the circumference of a circle is
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
The diameters of front and rear wheels of a tractor are 80 cm and 2 m respectively. Find the number of revolutions that rear wheel will make in covering a distance in which the front wheel makes 1400 revolutions.
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
