Advertisements
Advertisements
प्रश्न
The inner circumference of a circular track is 264 m and the width of the track is 7 m. Find:
(i) the radius of the inner track.
(ii) the radius of the outer circumference.
(iii) the length of the outer circumference.
(iv) the cost of fencing the outer circumference at the rate of ₹50 per m.
उत्तर
Inner circumference of the circular track = 264 m
(i) ∴ Inner radius (r) = `"C"/(2π)`
= `(264xx7)/(2xx22)=1848/44` = 42 cm
(ii) Width of the track = 7 m
∴ Outer radius (R) = 42 + 7 = 49 m
(iii) Outer circumference = 2πR
= `2xx22/7xx49` = 308 m
(iv) Rate of fencing = ₹50 per metre
∴ Total cost of fencing outer circumference = ₹50 × 308 = ₹15,400
APPEARS IN
संबंधित प्रश्न
If the perimeter of a semi-circular protractor is 66 cm, find the diameter of the protractor (Take π = 22/7).
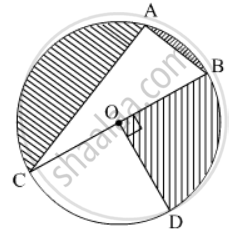
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region.
Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
Find the circumference and area of circle of radius 4.2 cm
A copper wire when bent in the form of a square encloses an area of 484 cm2. The same wire is not bent in the form of a circle. Find the area enclosed by the circle.
The side of a square is 10 cm. Find the area of the inscribed circle [π = 3.14]
The radius of a circular garden is 100 m. There is a road 10 m wide, running all around it. Find the area of the road and the cost of levelling it at Rs 20 per m2. [Use π = 3.14]
The area of the circle is given below; find the diameter.
176 sq cm
Sand from a cylindrical bucket 32 cm in height and 18 cm in radius is poured onto the ground making a conical heap 24 cm high. Find the radius of the conical heap.
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of 484 `sqrt3` cm2. If the same wire is bent into the form of a circle of largest area, find the area of this circle.
