Advertisements
Advertisements
Question
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

Solution

Radius of inner circle, OC = 21 cm
Radius of outer circle, OA = 42 cm
Area of a circle with radius R = `piR^2 = pi(42)^2`
Area of a circle with radius r = `pir^2 = pi(21)^2`
Area of sector AOB = `theta/360 xx piR^2 = 60/360 xx pi(42)^2 = (pi(42)^2)/6`
Area of sector COD = `theta/360 xx pir^2 = 60/360 xx pi(21)^2 = (pi(21)^2)/6`
Area of shaded portion = Area of circle with radius R - Area of circle with radius r - [Area of sector AOB - Area of sector COD]
= `pi(42)^2 - pi(21)^2 - [(pi(42)^2)/6 - (pi(21)^2)/6]`
= `pi[(42)^2 - (21)^2 - 1/6[(42)^2 - (21)^2]]`
= `pi[((42)^2 - (21)^2)(1 - 1/6)]`
= `pi[(42 - 21)(42 + 21)5/6]`
= `22/7 xx 5/6 xx 21 xx 63`
= 3465 cm2
APPEARS IN
RELATED QUESTIONS
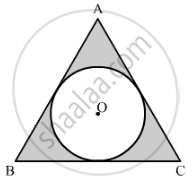
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
The minute hand of clock is10cm long. Find the area of the face of the clock described by the minute hand between 8am and 8:25 am
Choose the correct alternative answer for the following question.
Find the radius of a circle whose perimeter and area are numerically equal.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 16 cm , diameter = 24 cm
Find the area and perimeter of the following semi-circle :
Diameter= 7 cm
The wheel of a bullock cart has a diameter of 1.4 m. How many rotations will the wheel complete as the cart travels 1.1 km?
If the circumference of a circle is 352 metres, then its area in square metres is ____________.
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
The area of a square is 100 cm2. The circumference (in cm) of the largest circle cut of it is ______.
