Advertisements
Advertisements
Question
Choose the correct alternative answer for the following question.
Options
1 cm
10 cm
100 cm
1000 cm
Solution
100 cm
Explanation:
Volume of the cube = 1 m3
∴ (Side)3 = 1 m3 = (1 m)3
⇒ Side = 1 m = 100 cm
Thus, the side of the cube is 100 cm.
RELATED QUESTIONS
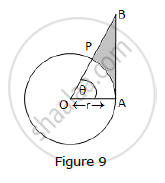
In Fig. 9, is shown a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OQ and meets OP produced at B. Prove that the perimeter of shaded region is
`r[tantheta+sectheta+(pitheta)/180-1]`
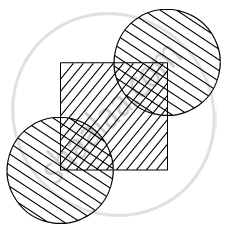
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.
A horse is tied to a pole with 28m long string. Find the area where the horse can graze.
A horse is placed for grazing inside a rectangular field 40m by 36m and is tethered to one corner by a rope 14m long. Over how much area can it graze.
In circle of radius 6cm, chord of length 10 cm makes an angle of 110° at the centre of circle find Area of the circle
A playground has the shape of rectangle, with two semicircles on its smaller sides as diameters, added to its outside. If the sides of rectangle are 36m and 24.5m. find the area of playground.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle.
The area of an equilateral triangle is `49sqrt(3)` cm2 . Taking each angular point as centre, circles are drawn with radius equal to half the length of the side of the triangle. Find the area of the triangle not included in the circles. [Take π = 1.73]
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Find the diameter of the sphere for the following :
Volume = `72pi "cm"^3`
The diameter of a circle is 28 cm.
Find its :
(i) Circumference
(ii) Area.
An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.
The radius of two circles are in the ratio 3 : 5, find the ratio between their circumferences.
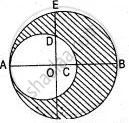
In the adjoining figure, the crescent is formed by two circles which touch at the point A. O is the centre of bigger circle. If CB = 9 cm and DE = 5 cm, find the area of the shaded portion.
The diameter of the wheel of a cart is 1.05 m. How much distance will the cart cover in 1000 rotations of the wheel?
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
The area of a circle whose circumference is 22 cm, is ____________.
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
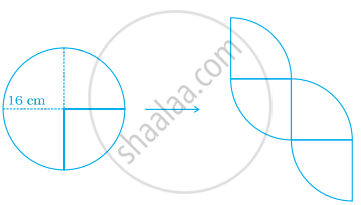
Does the perimeter change? If it does change, by how much does it increase or decrease?
