Advertisements
Advertisements
प्रश्न
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
उत्तर
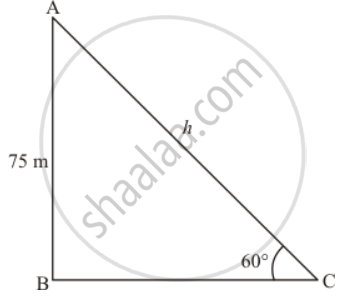
Let AC be the string of length, hm and C be the point, makes an angle of 60° and the kite is flying at the height of 75 m from the ground level.
In a triangle, ABC, given that height of kite is AB = 75 m and angle C = 60°
Now we have to find the length of the string.
So we use trigonometric ratios.
In a triangle ABC
`=> sin C = (AB)/(AC)`
`=> sin 60^@ = 75/h`
`=> sqrt3/2 = 75/h`
`=> h = 150/sqrt3`
Therefore h = 86.6
Hence length of string is 87 meters
APPEARS IN
संबंधित प्रश्न
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
The angle of elevation of the top of a tower from certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

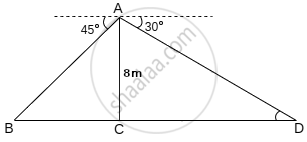
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
