Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be 100 m. State if the height of the above mentioned chimney meets the pollution norms. What value is discussed in this question?
उत्तर
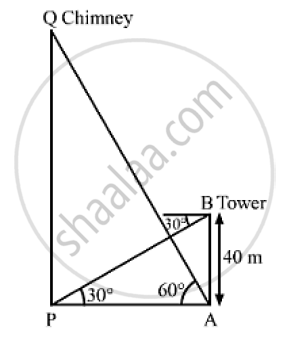
Let PQ be the chimney and AB be the tower.
We have,
AB = 40m,∠APB = 30° and ∠PAQ = 60°
In ΔABP,
`tan 30° = (AB)/(AP)`
`⇒ 1/ sqrt(3) = 40/ (AP)`
`⇒ AP = 40 sqrt(3 ) m`
Now, in Δ APQ ,
` tan 60° = (OQ)/(AP)`
`⇒ sqrt(3) = (PQ) / (40 sqrt(3))`
∴ PQ = 120 m
So, the height of the chimney is 120 m.
Hence, the height of the chimney meets the pollution norms.
In this question, management of air pollution has been shown
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
A tower is 100√3 metres high. Find the angle of elevation of its top from a point 100 metres away from its foot.
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
