Advertisements
Advertisements
Question
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Solution
Let the coordinates of the vertices P and R of ∆PQR be (a1, b1) and (a2, b2), respectively.
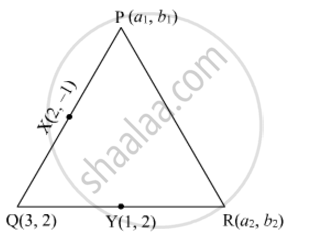
Suppose X(2, −1) is the midpoint of PQ.
Then,
`(2,-1)=((a_1+3)/2, (b_1+2)/2)`
`=>(a_1+3)/2=2 `
⇒ a1=1 and b1=−4
Therefore, the coordinates of P are (1, −4).
Again, suppose Y(1, 2) is the midpoint of QR.
Now,
`(1,2)=((a_2+3)/2,(b_2+2)/2)`
`=>(a_2+3)/2=1 `
⇒ a2=−1 and b2=2
Therefore, the coordinates of R are (−1, 2).
Thus, the vertices of ∆PQR are P(1,−4), Q(3, 2) and R(−1, 2).
Now,
Area of ∆PQR =`1/2`×[1(2−2)+3(2+4)−1(−4−2)]
=`1/2`(18+6)
=`1/2`(24)
=12
Thus, the area of ∆PQR is 12 square units.
RELATED QUESTIONS
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
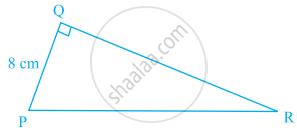
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.