Advertisements
Advertisements
Question
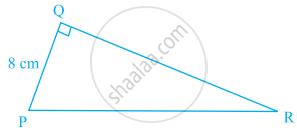
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
Solution
Given, area of ΔPOR = 60 cm2 and side PQ = 8 cm
∴ Area of ΔPQR = `1/2` × PQ × QR ......[∵ Area of triangle = Base × Height]
⇒ 60 = `1/2` × 8 × QR
⇒ QR = `(60 xx 2)/8`
⇒ QR = 15 cm
In right-angled ΔPOR, PR2 + PQ2 + QR2 ......[By Pythagoras theorem]
⇒ PR2 + 82 + 152 = 64 + 225
⇒ PR2 = 289
⇒ PR = `sqrt(289)` = 17 cm
Hence, the length of two sides are 15 cm and 17 cm.
APPEARS IN
RELATED QUESTIONS
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
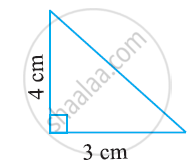
Find the area of the following triangle:
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
