Advertisements
Advertisements
प्रश्न
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
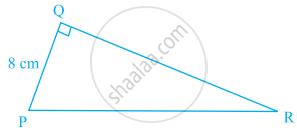
उत्तर
Given, area of ΔPOR = 60 cm2 and side PQ = 8 cm
∴ Area of ΔPQR = `1/2` × PQ × QR ......[∵ Area of triangle = Base × Height]
⇒ 60 = `1/2` × 8 × QR
⇒ QR = `(60 xx 2)/8`
⇒ QR = 15 cm
In right-angled ΔPOR, PR2 + PQ2 + QR2 ......[By Pythagoras theorem]
⇒ PR2 + 82 + 152 = 64 + 225
⇒ PR2 = 289
⇒ PR = `sqrt(289)` = 17 cm
Hence, the length of two sides are 15 cm and 17 cm.
APPEARS IN
संबंधित प्रश्न
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
