Advertisements
Advertisements
प्रश्न
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
उत्तर
| Base | Height | Area of parallelogram |
| 5.8 | 8.4 cm | 48.72 cm2 |
Explanation:
b = ?
h = 8.4 cm
Area = 48.72 cm2
b × 8.4 = 48.72
b = `48.72/8.4`
b = 5.8 cm
Therefore, the base of such parallelogram is 5.8 cm.
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Find the area of the following triangle:
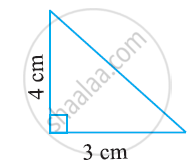
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
