Advertisements
Advertisements
प्रश्न
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
उत्तर
Let the given line divide the line segment joining the points A(2, −2) and B(3, 7) in a ratio k : 1
Coordinates of the point of division = ` ((3k+2)/(k+1), (7k-2)/(k+1))`
This point also lies on 2x + y − 4 = 0
`:.2((3k+2)/(k+1))+((7k-2)/(k+1))-1=0`
`=>(6k+4+7k-2-4k-4)/(k+1)=0`
`=>9k-2=0`
`=>k=2/9`
Therefore, the ratio in which the line 2x + y − 4 = 0 divides the line segment joining the points A(2, −2) and B(3, 7) is 2:9.
APPEARS IN
संबंधित प्रश्न
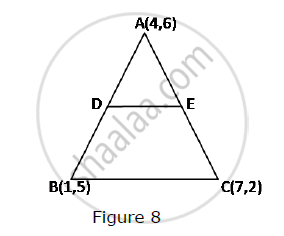
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
If the points P(–3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, find the values of a and b.
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
If `a≠ b ≠ c`, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
