Advertisements
Advertisements
प्रश्न
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
उत्तर
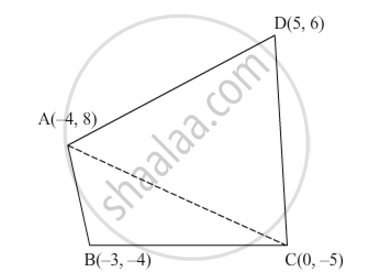
Let the vertices of the quadrilateral be A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6).
Join AC to form two triangles, namely, ΔABC and ΔACD.
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
We know
Area of triangle having vertices (x1, y1), (x2, y2) and (x3, y3) =`1/2`[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
Now,
Area of ∆ABC=`1/2`{(−4)[(−4)−(−5)]+(−3)[(−5)−(8)]+(0)[(8)−(−4)]}
=`1/2`(−4+39)
`=35/2 `
Area of ∆ACD=`1/2`{(−4)[(−5)−(6)]+(0)[(6)−(8)]+(5)[(8)−(−5)]}
=`1/2`(44+65)
`=109/2`
∴Area of quadrilateral ABCD=Area of ∆ABC+Area of ∆ACD
`35/2+109/2`
=72 square units
Thus, the area of quadrilateral ABCD is 72 square units.
संबंधित प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
If `a≠ b ≠ c`, prove that the points (a, a2), (b, b2), (c, c2) can never be collinear.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
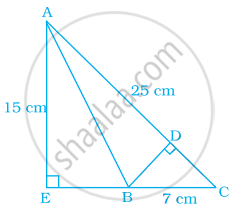
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.