Question

A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment.

Answer 1

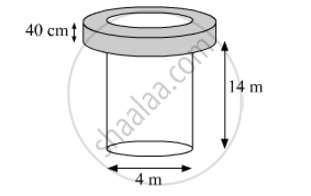
Depth (h₁) of the well = 14 m

Radius (r₁) of the circular end of the well =`4/2` m = 2 m

Height (h₂) of embankment = 40 cm = 0.4 m

Let the width of embankment be x.

From the figure, it can be observed that the embankment will be cylindrical in shape having outer radius (r₂) as (2 + x) m and inner radius (r₁) as 2 m.

Volume of earth dug from the well = Volume of earth used to form embankment

`pir_1^2h_1=pi(r_2^2-r_1^2)h_2`

`=>pi(2)^2 14=pi[(2+x)^2-2^2]0.4`

`=>4xx14=(x(x+4)4)/10`

⇒x²+4x−140=0

⇒x²+14x−10x−140=0

⇒(x+14)(x−10)=0

⇒x=10                (Because x cannot be negative)

Therefore, the width of the embankment will be 10 m.