Advertisements
Advertisements
प्रश्न
A solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm.Find the number of cones so formed.
उत्तर
Let the number of cones formed be n.
Given: Radius of sphere, r = 10.5 cm
Volume of sphere`V_1=pi_3^4-r^3`
`rArrV rpi_3^4-(10.5)cm^3`
Given: Height of cone, h = 3 cm and radius of cone, R = 3.5 cm
`therefore` Volume of each smaller come `v_2=1/3piR^2h`
`rArr V_2=1/3pi(3.5)^2xx3cm^3`
Since the solid sphere is melted and recast into smaller cones,
n × Volume of each smaller cone = Volume of the sphere
`thereforenxx1/3 pi (3.5)^2xx3=4/3pi(10.5)^3`
`rArrn=(4xx(10.5)^3)/((3.5)^2xx3)`
`rArrn=126`
Thus, the number of smaller cones formed is 126.
APPEARS IN
संबंधित प्रश्न
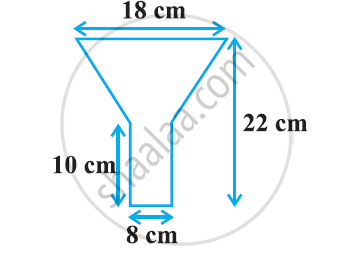
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given figure).
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube?
The volume of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
A cylindrical pencil sharpened at one end is a combination of
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is ______.
The sum of length, breadth and height of a cuboid is 19 cm and its diagonal is `5sqrt(5)` cm. Its surface area is
A running track has 2 semicircular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
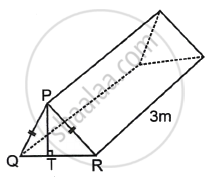
A tent is a shape of a triangular 'prism' resting on a rectangular side PQ = PR, PT = 1.5 m, QR = 1.8 m, length of the tent = 3 m. Find:
- ∠PQR
- The volume of the tent