Advertisements
Advertisements
प्रश्न
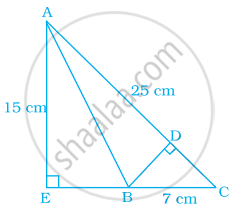
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.
उत्तर
Given, AC = 25 cm, BC = 7 cm, and AE = 15 cm
In ΔAEC, using Pythagoras theorem,
AC2 = AE2 + EC2
⇒ EC2 = AC2 – AE2
⇒ EC2 = (25)2 – (15)2 = 625 – 225 = 400
EC = `sqrt(400)` = 20 cm
and EB = EC – BC = 20 – 7 = 13 cm
Area of ΔAEC = `1/2` × AE × EC
= `1/2 xx 15 xx 20`
= 150 cm2
and Area of ΔAEB = `1/2` × AE × EB
= `1/2 xx 15 xx 13`
= 97.5 cm2
∴ Area of ΔABC = Area of ΔAEC – Area of ΔAEB
= 150 – 97.5
= 52.5 cm2
Again, Area of ΔABC = `1/2` × BD × AC
52.5 = `1/2` × BD × 25
⇒ BD = `(52.5 xx 2)/25` = 4.2 cm
Hence, the area of ΔABC is 52.5 cm2 and the length of DB is 4.2 cm.
APPEARS IN
संबंधित प्रश्न
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Show that the points are the vertices of an isosceles right triangle.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
Area of triangle MNO in the figure is ______.
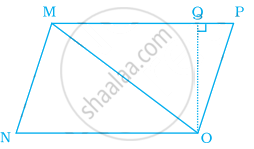
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

