Advertisements
Advertisements
प्रश्न
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
उत्तर
Area of a triangle = `1/2 abs ((x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1))`
`=> 1/2 abs ((-2,0,1),(0,4,1),(0, k,1))`
`= 1/2 [-2 (4 - k) - 0 (0 - 0) + 1 (0 - 0)]`
`= 1/2 xx (-2) (4 - k)`
= k - 4
= `pm 4`
When, k - 4 = 4, `therefore k = 8`
k - 4 = 4 `therefore k = 0`
APPEARS IN
संबंधित प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find a relation between x and y if the points (x, y), (1, 2) and (7, 0) are collinear.
Find equation of line joining (3, 1) and (9, 3) using determinant.
Find the area of the following triangle:
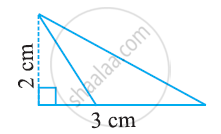
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
Show that the following points are collinear:
A(8,1), B(3, -4) and C(2, -5)
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
Find the area of the following triangle:

Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
Show that the ∆ABC is an isosceles triangle if the determinant
Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
The points (1,1), (-2, 7) and (3, -3) are ______.
The points (0, 5), (0, –9) and (3, 6) are collinear.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Area of triangle MNO in the figure is ______.
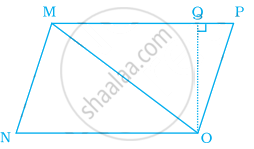
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
