Advertisements
Advertisements
प्रश्न
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
उत्तर
Joining B to D, we get two triangles ABD and BCD.
Area of ΔABD = `1/2 [-5(-5-5) - 4(5-7)+4(7+5)]`
`= 1/2 (50 + 8 + 48)`
`= 106/2`
= 53 sq units
Area of ΔBCD = `1/2 [-4(-6-5) - 1(5 + 5) + 4(-5 + 6)]`
`= 1/2 (44 - 10 + 4)`
`= 38/2`
= 19 sq units.
∴ Area of quad. ABCD = Area of ∆ABD + Area of ∆BCD = 53 + 19 = 72 sq units.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
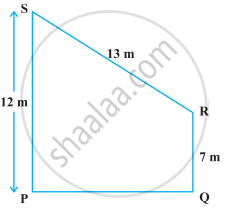
Find the area of the trapezium PQRS with height PQ given in the following figure.