Question

The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)

Answer 1

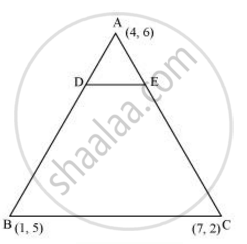
Given that (AD)/(AB) = (AE)/(AC) = 1/4

(AD)/(AD+DB) = (AE)/(AE+EC) = 1/4

(AD)/(DB)=(AE)/(EC) = 1/3

Therefore, D and E are two points on side AB and AC respectively such that they divide side AB and AC in a ratio of 1:3

Coordinates of Point D =`((1xx1+3xx4)/(1+3),(1xx5+3xx6)/(1+3))`

`= (13/4, 23/4)`

Coordinates of Point E =`((1xx7+3xx4)/(1+3), (1xx2+3xx6)/(1+3))`

`= (19/4, 20/4)`

Area of triangle =`1/2[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`

Area of ΔADE =`1/2[4(23/4-20/4)+13/4(20/4-6)+19/4(6-23/4)]`

`=1/2[3-13/4+19/16] = 1/2[(48-52+19)/16] = 15/32 `

Area of ΔABC =`1/2[4(5-2)+1(2-6)+7(6-5)]`

`= 1/2[12-4+7] = 15/2 `

Clearly, the ratio between the areas of ΔADE and ΔABC is 1:16.

Alternatively,

We know that if a line segment in a triangle divides its two sides in the same ratio, then the line segment is parallel to the third side of the triangle. These two triangles so formed (here ΔADE and ΔABC) will be similar to each other.

Hence, the ratio between the areas of these two triangles will be the square of the ratio between the sides of these two triangles.

Therefore, ratio between the areas of ΔADE and ΔABC  =` (1/4)^2 = 1/16`