Advertisements
Advertisements
प्रश्न
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
उत्तर १
The Vertices of ΔABC are A (2, 3), B (3, 5), and C (4, 4)
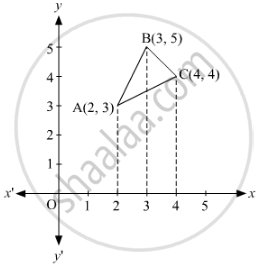
Equation of line segment AB is
`("y" - 5) = (5-3)/(3-2) ("x" -3)`
=`"y" -5 = 2 ("x" -3)`
=`"y" = 2"x" -1`
Equation of line segment BC is
`("y" - 5) = (5-3)/(3-4) ("x" -3)`
=`"y" -5 = -1 ("x" -3)`
=`"y" = -"x" + 8`
Equation of line segment AC is
`("y" - 4) = (4-3)/(4-2) ("x" -4)`
=`"y" -4 = (1)/(2) ("x" -4)`
= `"y" = ("x")/(2) + 2`
∴ Area of ΔABC = `int_2^3 [(2"x" -1) - ("x"/2+2)] d"x" + int_3^4 [(-"x" + 8) - ("x"/2 + 2)] . d"x"`
= `int_2^3 ((3"x")/2 -3) . d"x" + int_3^4 ((-3"x")/2 + 6) . d"x"`
= `[(3"x"^2)/(4) - 3"x"]_2^3 + [ (-3"x"^2)/4 + 6"x"]_3^4`
= `(27/4 - 9) - (3 -6) + (-12 + 24) - (-27/4 + 18)`
= `(3)/(2) "sq. units"`.
उत्तर २
The Vertices of ΔABC are A (2, 3), B (3, 5), and C (4, 4)
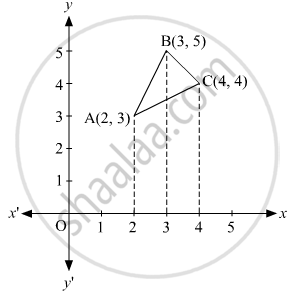
Equation of line segment AB is
`("y" - 5) = (5-3)/(3-2) ("x" -3)`
=`"y" -5 = 2 ("x" -3)`
=`"y" = 2"x" -1`
Equation of line segment BC is
`("y" - 5) = (5-3)/(3-4) ("x" -3)`
=`"y" -5 = -1 ("x" -3)`
=`"y" = -"x" + 8`
Equation of line segment AC is
`("y" - 4) = (4-3)/(4-2) ("x" -4)`
=`"y" -4 = (1)/(2) ("x" -4)`
= `"y" = ("x")/(2) + 2`
∴ Area of ΔABC = `int_2^3 [(2"x" -1) - ("x"/2+2)] d"x" + int_3^4 [(-"x" + 8) - ("x"/2 + 2)] . d"x"`
= `int_2^3 ((3"x")/2 -3) . d"x" + int_3^4 ((-3"x")/2 + 6) . d"x"`
= `[(3"x"^2)/(4) - 3"x"]_2^3 + [ (-3"x"^2)/4 + 6"x"]_3^4`
= `(27/4 - 9) - (3 -6) + (-12 + 24) - (-27/4 + 18)`
= `(3)/(2) "sq. units"`.
APPEARS IN
संबंधित प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Find equation of line joining (3, 1) and (9, 3) using determinant.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the area of the following triangle:

ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

Find the area of the following triangle:

If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
