Advertisements
Advertisements
प्रश्न
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
उत्तर
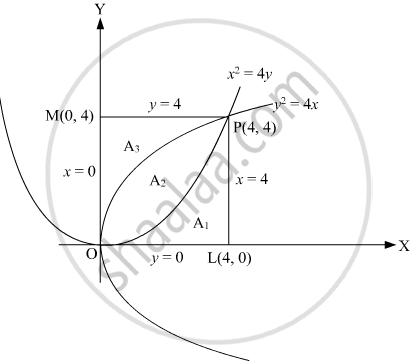
A(OABC) = 4 × 4 = 16 sq. units
From, y2 = 4x and x2 = 4y
`(x^2/4)^2 = 4x`
or `x^4/16 = 4x`
or x4 - 64x = 0
or x(x3 - 64) = 0
or x = 0 or x = 4
when x = 0, y = 0
x = 4, y = 4
Point of intersection of the two parabolas is (0, 0) and (4, 4).
Area of part III = `int_0^4 y dx` (parabola x2 = 4y)
= `int_0^4 (x^2)/4 dx = [1/4 x^3/3]_0^4`
= `1/12(64 - 0)`
= `64/12`
= `16/3` sq.units
Area of I = Area of square - Area of II and III
= `16 - int_0^4 sqrt(4x) dx`
= `16 - (2 × 2)/3 [x^(3/2)]_0^4`
= `16 - 32/3` sq. units
= `16/3` sq. units
Area of II = Area of square - Area of I - Area of III
= 16 - `16/3 - 16/3` sq. units
= `16/3` sq. units
The two curves divide the square into three equal parts.
संबंधित प्रश्न
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by the curve \[a y^2 = x^3\], the y-axis and the lines y = a and y = 2a.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Make a sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 3; 0 ≤ y ≤ 2x + 3; 0 ≤ x ≤ 3} and find its area using integration.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area of the region formed by x2 + y2 − 6x − 4y + 12 ≤ 0, y ≤ x and x ≤ 5/2 is ______ .
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
The area enclosed by y2 = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
