Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
उत्तर
The intersecting points of the given curves are obtained by solving the equations x – y = 4 and y2 = 2x for x and y.
We have y2 = 8 + 2y
i.e., (y – 4)(y + 2) = 0
Which gives y = 4, –2 and x = 8, 2.
Thus, the points of intersection are (8, 4), (2, –2).
Hence Area = `int_(-2)^4 (4 + y - 1/2 y^2)"d"y`
= `|4y + y^2/2 - 1/6 y^3|_-2^4`
= 18 sq.units.
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Using the method of integration find the area of the region bounded by lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the curves y = sin x between the ordinates x = 0, x = π and the x-axis is _____________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.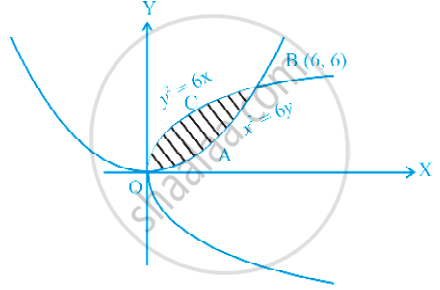
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Using integration, find the area of the region bounded by line y = `sqrt(3)x`, the curve y = `sqrt(4 - x^2)` and Y-axis in first quadrant.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
