Advertisements
Advertisements
प्रश्न
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
उत्तर
The parabola \[y^2 = 4ax\] opens towards the positive x-axis and its focus is (a, 0).
The line y = mx passes through the origin (0, 0).
Solving \[y^2 = 4ax\] and y = mx, we get
\[m^2 x^2 = 4ax\]
\[ \Rightarrow m^2 x^2 - 4ax = 0\]
\[ \Rightarrow x\left( m^2 x - 4a \right) = 0\]
\[ \Rightarrow x = 0\text{ or }x = \frac{4a}{m^2}\]
So, the points of intersection of the given parabola and line are O(0, 0) and
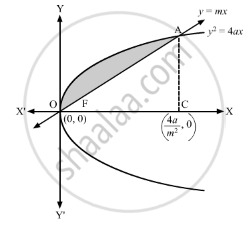
∴ Area bounded by the given parabola and line
= Area of the shaded region
\[= \int_0^\frac{4a}{m^2} y_{\text{ parabola }} dx - \int_0^\frac{4a}{m^2} y_{\text{ line }} dx\]
\[ = \int_0^\frac{4a}{m^2} \sqrt{4ax}dx - \int_0^\frac{4a}{m^2} mxdx\]
\[ = \left.2\sqrt{a} \times \frac{x^\frac{3}{2}}{\frac{3}{2}}\right|_0^\frac{4a}{m^2} - \left.m \times \frac{x^2}{2}\right|_0^\frac{4a}{m^2} \]
\[ = \frac{4\sqrt{a}}{3}\left[ \left( \frac{4a}{m^2} \right)^\frac{3}{2} - 0 \right] - \frac{m}{2}\left[ \left( \frac{4a}{m^2} \right)^2 - 0 \right]\]
\[ = \frac{4\sqrt{a}}{3} \times \frac{8a\sqrt{a}}{m^3} - \frac{m}{2} \times \frac{16 a^2}{m^4}\]
\[ = \frac{32 a^2}{3 m^3} - \frac{8 a^2}{m^3}\]
\[ = \frac{8 a^2}{3 m^3}\text{ square units }\]
But,
Area bounded by the given parabola and line = \[\frac{a^2}{12}\] sq. units ............(Given)
\[\therefore \frac{8 a^2}{3 m^3} = \frac{a^2}{12}\]
\[ \Rightarrow m^3 = 32\]
\[ \Rightarrow m = \sqrt[3]{32}\]
Thus, the value of m is \[\sqrt[3]{32}\]
APPEARS IN
संबंधित प्रश्न
Using the method of integration, find the area of the triangular region whose vertices are (2, -2), (4, 3) and (1, 2).
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices area A(1, 2), B (2, 0) and C (4, 3).
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
