Advertisements
Advertisements
प्रश्न
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
उत्तर
Given the equation of the ellipse is `"x"^2/9+"y"^2/4=1`
Let `"y"_1=2/3sqrt(9-"x"^2)` and
equation of the line is `"x"/3+"y"/2=1`
Let `"y"_2=2/3(3-"x")`
we have (3, 0) and (0, 2) as the points of intersection of ellipse and line.
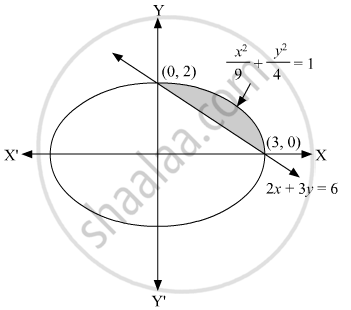
Therefore, the area of a smaller region, A `=int_0^3("y"_1-"y"_2)"dx"`
`"A" =int_0^3[2/3sqrt(9-"x"^2)-2/3(3-"x")]"dx"`
`=int_0^3(2/3sqrt(9-"x"^2))"dx"-int_0^3[2/3(3-"x")]"dx"`
`=2/3["x"/2sqrt(9-"x"^2)+9/2sin^-1("x"/3)]_0^3-2/3(3"x"-"x"^2/2)_0^3`
`=2/3[(0+9/2xxpi/2)-0]-2/3(9-9/2-0)`
`=((3pi)/2-3)` sq. unit
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
The area bounded by the curve y = x | x|, x-axis and the ordinates x = –1 and x = 1 is given by ______.
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
Draw a rough sketch of the curve and find the area of the region bounded by curve y2 = 8x and the line x =2.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Prove that the area common to the two parabolas y = 2x2 and y = x2 + 4 is \[\frac{32}{3}\] sq. units.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the area of the region included between y2 = 9x and y = x
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Make a rough sketch of the region {(x, y): 0 ≤ y ≤ x2, 0 ≤ y ≤ x, 0 ≤ x ≤ 2} and find the area of the region using integration.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Make a rough sketch of the region {(x, y) : 0 ≤ y ≤ x2 + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
