Advertisements
Advertisements
प्रश्न
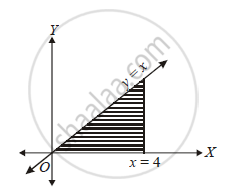
triangle bounded by the lines y = 0, y = x and x = 4 is revolved about the X-axis. Find the volume of the solid of revolution.
उत्तर
Given line is y = x
`V=piint_0^4 y^2dx`
`=pi int_0^4x^2dx`
`=pi/3[x^3]_0^4`
`=(64pi)/3 cubic units.`
APPEARS IN
संबंधित प्रश्न
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area of the region enclosed by it, using integration.
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Using integration, find the area of the triangular region, the equations of whose sides are y = 2x + 1, y = 3x+ 1 and x = 4.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area included between the parabolas y2 = 4x and x2 = 4y is (in square units)
The area bounded by the parabola y2 = 4ax and x2 = 4ay is ___________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
