Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
उत्तर
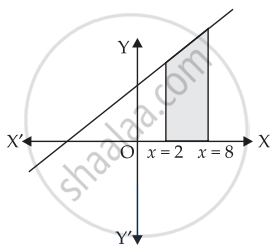
Given that: 2y = 5x + 7, x-axis, x = 2 and x = 8.
Let us draw the graph of 2y = 5x + 7
⇒ y = `(5x + 7)/2`
| x | 1 | –1 |
| y | 6 | 1 |
Area of the required shaded region
= `int_2^8 ((5x + 7)/2) "d"x`
= `1/2[5/2 x^2 + 7x]_2^8`
= `1/2[5/2 (64 - 4) + 7(8 - 2)]`
= `1/2[5/2 xx 60 + 7 xx 6]`
= `1/2[150 + 42]`
= `1/2 xx 192`
= 96 sq.units
Hence, the required area = 96 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Draw a rough sketch of the graph of the function y = 2 \[\sqrt{1 - x^2}\] , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region common to the circle x2 + y2 = 16 and the parabola y2 = 6x.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
