Advertisements
Advertisements
प्रश्न
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
उत्तर

Let the two curves be named as y1 and y2 where
\[y_1 : \left( x - 3 \right)^2 + y^2 = 9 . . . . . \left( 1 \right)\]
\[ y_2 : x^2 + y^2 = 9 . . . . . \left( 2 \right)\]
The curve x2 + y2 = 9 represents a circle with centre (0, 0) and the radius is 3.
The curve (x − 3)2 + y2 = 9 represents a circle with centre (3, 0) and has a radius 3.
To find the intersection points of two curves equate them.
On solving (1) and (2) we get
Therefore, intersection points are
Now, the required area (OABO) =2 [area(OACO) +area (CABC)]
Here,
Thus the required area is given by,
A = 2 [area(OACO) +area(CABC)]
Hence the required area is \[6\pi - \frac{9\sqrt{3}}{2}\] square units.
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Sketch the graph y = | x + 3 |. Evaluate \[\int\limits_{- 6}^0 \left| x + 3 \right| dx\]. What does this integral represent on the graph?
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region {(x, y) : y2 ≤ 8x, x2 + y2 ≤ 9}.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area of the region bounded by the parabola y2 = 2x + 1 and the line x − y − 1 = 0.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.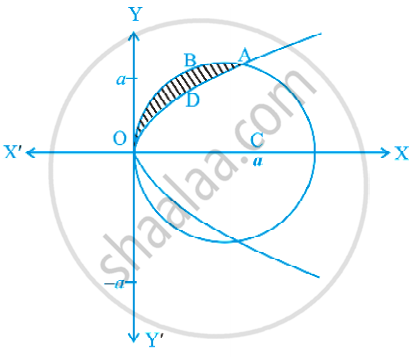
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Area of the region bounded by the curve `y^2 = 4x`, `y`-axis and the line `y` = 3 is:
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
Let the curve y = y(x) be the solution of the differential equation, `("dy")/("d"x) = 2(x + 1)`. If the numerical value of area bounded by the curve y = y(x) and x-axis is `(4sqrt(8))/3`, then the value of y(1) is equal to ______.
