Question

The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.

विकल्प

• 20π sq.unit

• 20π² sq.units

• 16π² sq.units

• 25π sq.units

Answer 1

The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is 20π sq.unit.

Explanation: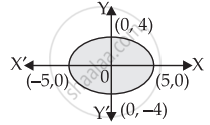

Given equation of ellipse is `x^2/25 + y^2/16` = 1

⇒ `y^2/16 = 1 - x^2/25`

⇒ y² = `16/25 (25 - x^2)`

∴ y = `4/5 sqrt(25 - x^2)`

∴ Since the ellipse is symmetrical about the axes.

∴ Required area = `4 xx int_0^5 4/5 sqrt(25 - x^2)  "d"x`

= `4 xx 4/5 int_0^5 sqrt((5)^2 - x^2)  "d"x`

= `6/5 [x/2 sqrt((5)^2 - x^2) + 25/2 sin^-1  x/5]_0^5`

= `16/5 [0 + 25/2 * sin^-1 (5/5) - 0 - 0]`

= `16/5 [25/2 * sin^-1 (1)]`

= `16/5 [25/2 * pi/2]`

= 20π sq.unit