Advertisements
Online Mock Tests
Chapters
2: Inverse Trigonometric Functions
3: Matrices
4: Determinants
5: Continuity And Differentiability
6: Application Of Derivatives
7: Integrals
▶ 8: Application Of Integrals
9: Differential Equations
10: Vector Algebra
11: Three Dimensional Geometry
12: Linear Programming
13: Probability
![NCERT Exemplar solutions for Mathematics [English] Class 12 chapter 8 - Application Of Integrals NCERT Exemplar solutions for Mathematics [English] Class 12 chapter 8 - Application Of Integrals - Shaalaa.com](/images/mathematics-english-class-12_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 8: Application Of Integrals
Below listed, you can find solutions for Chapter 8 of CBSE NCERT Exemplar for Mathematics [English] Class 12.
NCERT Exemplar solutions for Mathematics [English] Class 12 8 Application Of Integrals Solved Examples [Pages 170 - 176]
Short Answer
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.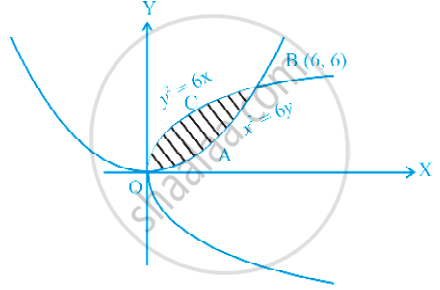
Find the area enclosed by the curve x = 3 cost, y = 2 sint.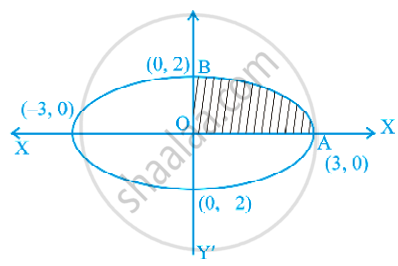
Long Answer
Find the area of the region included between the parabola y = `(3x^2)/4` and the line 3x – 2y + 12 = 0.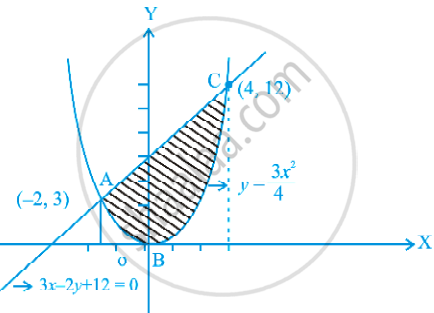
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.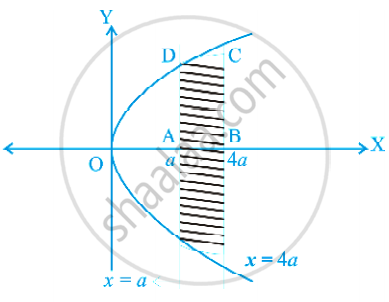
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.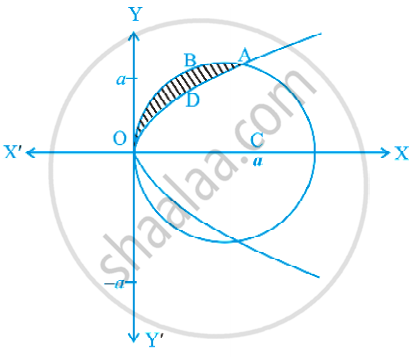
Find the area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = `"a"/2`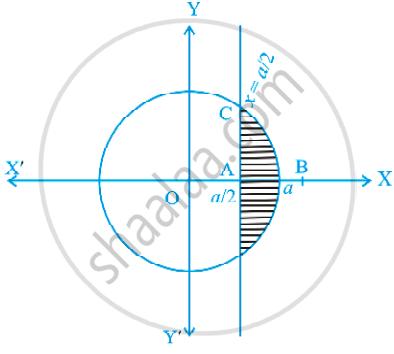
Objective Type Questions from 10 to 12
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
4π sq.units
`2sqrt(2)pi` sq.units
4π2 sq.units
2π sq.units
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
π2ab
πab
πa2b
πab2
The area of the region bounded by the curve y = x2 and the line y = 16 ______.
`32/3`
`256/3`
`64/3`
`128/3`
Fill in the blanks 13 and 14
The area of the region bounded by the curve x = y2, y-axis and the line y = 3 and y = 4 is ______.
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
NCERT Exemplar solutions for Mathematics [English] Class 12 8 Application Of Integrals Exercise [Pages 176 - 178]
Short Answer
Find the area of the region bounded by the curves y2 = 9x, y = 3x
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area of the region included between y2 = 9x and y = x
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Calcualte the area under the curve y = `2sqrt(x)` included between the lines x = 0 and x = 1
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x- axis and the lines x = 2 and x = 8.
Draw a rough sketch of the curve y = `sqrt(x - 1)` in the interval [1, 5]. Find the area under the curve and between the lines x = 1 and x = 5.
Determine the area under the curve y = `sqrt("a"^2 - x^2)` included between the lines x = 0 and x = a.
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
Long Answer
Find the area of the region bounded by the curve y2 = 2x and x2 + y2 = 4x.
Find the area bounded by the curve y = sinx between x = 0 and x = 2π.
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
Compute the area bounded by the lines x + 2y = 2, y – x = 1 and 2x + y = 7.
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Objective Type Questions from 24 to 34
The area of the region bounded by the y-axis, y = cosx and y = sinx, 0 ≤ x ≤ `pi/2` is ______.
`sqrt(2)` sq.units
`(sqrt(2) + 1)` sq.units
`(sqrt(2) - 1)` sq.units
`(2sqrt(2) - 1)` sq.units
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
`3/8` sq.units
`5/8` sq.units
`7/8` sq.units
`9/8` sq.units
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
8 sq.units
20π sq.units
16π sq.units
256π sq.units
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
16π sq.units
4π sq.units
32π sq.units
24 sq.units
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
2 sq.units
4 sq.units
3 sq.units
1 sq.units
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
`4/3`sq.units
1 sq.units
`2/3`sq.units
`1/3`sq.units
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
2 sq.units
4 sq.units
3 sq.units
1 sq.unit
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
20π sq.unit
20π2 sq.units
16π2 sq.units
25π sq.units
The area of the region bounded by the circle x2 + y2 = 1 is ______.
2π sq.units
π sq.units
3π sq.units
4π sq.units
The area of the region bounded by the curve y = x + 1 and the lines x = 2 and x = 3 is ______.
`7/2` sq.units
`9/2` sq.units
`11/2` sq.units
`13/2` sq.units
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
4 sq.units
`3/2` sq units
6 sq.units
8 sq.units
Solutions for 8: Application Of Integrals
![NCERT Exemplar solutions for Mathematics [English] Class 12 chapter 8 - Application Of Integrals NCERT Exemplar solutions for Mathematics [English] Class 12 chapter 8 - Application Of Integrals - Shaalaa.com](/images/mathematics-english-class-12_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [English] Class 12 chapter 8 - Application Of Integrals
Shaalaa.com has the CBSE Mathematics Mathematics [English] Class 12 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [English] Class 12 CBSE 8 (Application Of Integrals) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 12 chapter 8 Application Of Integrals are Area of the Region Bounded by a Curve and a Line, Area Between Two Curves, Area Under Simple Curves.
Using NCERT Exemplar Mathematics [English] Class 12 solutions Application Of Integrals exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [English] Class 12 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 8, Application Of Integrals Mathematics [English] Class 12 additional questions for Mathematics Mathematics [English] Class 12 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
