Advertisements
Advertisements
प्रश्न
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
उत्तर
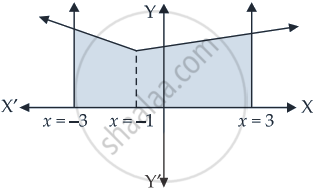
Given equations are y = 1 + |x + 1|
x = –3 and x = 3
y = 0
Taking y = 1 + |x + 1|
⇒ y = 1 + x + 1
⇒ y = x + 2
And y = 1 – x – 1
⇒ y = –x
On solving we get x = –1
Area of the required regions = `int_(-3)^(-1) -x "d"x + int_(-1)^3 (x + 2) "d"x`
= `-[x^2/2]_-3^-1 + [x^2/2 + 2x]_1^3`
= `-[1/2 - 9/2] + [(9/2 + 6) - (1/2 - 2)]`
= `-(-4) + [21/2 + 3/2]`
= 4 + 12
= 16 sq.units
Hence, the required area = 16 sq.units
APPEARS IN
संबंधित प्रश्न
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Find the area bounded by the curve y = cos x, x-axis and the ordinates x = 0 and x = 2π.
Find the area enclosed by the curve x = 3cost, y = 2sin t.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
If the area above the x-axis, bounded by the curves y = 2kx and x = 0, and x = 2 is \[\frac{3}{\log_e 2}\], then the value of k is __________ .
The area bounded by the parabola y2 = 4ax, latusrectum and x-axis is ___________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3, is
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
