Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
उत्तर

\[x^2 = 16 y\text{ is a parabola, with vertex at O}\left( 0, 0 \right)\text{ and symmetrical about + ve }y -\text{ axis }\]
\[y =\text{ 1 is line parallel to }x -\text{ axis cutting the parabola at }\left( - 4, 1 \right)\text{ and }\left( 4, 1 \right)\]
\[ y = 4\text{ is line parallel to }x \text{ axis cutting the parabola at }\left( - 8, 1 \right)\text{ and }\left( 8, 1 \right)\]
\[\text{ Consider a horizontal strip of length }= \left| x \right| \text{ and width }= dy\]
\[ \therefore\text{ Area of approximating rectangle }= \left| x \right| dy\]
\[\text{ The approximating rectangle moves from }y = 1\text{ to } y = 4\]
\[\text{ Area of the curve in the first quadrant enclosed by }y = 1\text{ and }y = 4\text{ is the shaded area }\]
\[ \therefore \text{ Area of the shaded region }= \int_1^4 \left| x \right| dy\]
\[ \Rightarrow A = \int_1^4 x dy ...............\left[ As, x > 0, \left| x \right| = x \right]\]
\[ \Rightarrow A = \int_1^4 \sqrt{16 y} dy\]
\[ \Rightarrow A = 4 \int_1^4 \sqrt{y} dy\]
\[ \Rightarrow A = 4 \left[ \frac{y^\frac{3}{2}}{\frac{3}{2}} \right]_1^4 \]
\[ \Rightarrow A = \frac{8}{3}\left[ 4^\frac{3}{2} - 1^\frac{3}{2} \right]\]
\[ \Rightarrow A = \frac{8}{3} \times 7 = \frac{56}{3}\text{ sq . units }\]
\[ \therefore\text{ Area enclosed by parabola in the first quadrant and }y = 1\text{ and }y = 4\text{ is }\frac{56}{3}\text{ sq . units }\]
APPEARS IN
संबंधित प्रश्न
Using integration, find the area bounded by the curve x2 = 4y and the line x = 4y − 2.
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Compare the areas under the curves y = cos2 x and y = sin2 x between x = 0 and x = π.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region bounded by the curve \[x = a t^2 , y = 2\text{ at }\]between the ordinates corresponding t = 1 and t = 2.
Find the area of the region in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1 and y = 4.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Using integration, find the area of the triangle ABC coordinates of whose vertices are A (4, 1), B (6, 6) and C (8, 4).
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
If the area bounded by the parabola \[y^2 = 4ax\] and the line y = mx is \[\frac{a^2}{12}\] sq. units, then using integration, find the value of m.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Find the coordinates of a point of the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x − 3.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.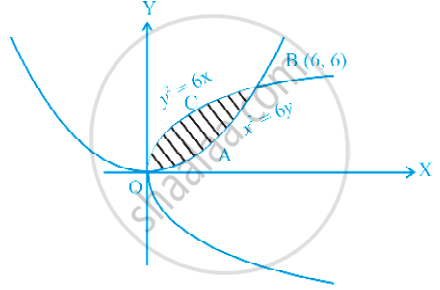
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
Find the area bounded by the lines y = 4x + 5, y = 5 – x and 4y = x + 5.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
If a and c are positive real numbers and the ellipse `x^2/(4c^2) + y^2/c^2` = 1 has four distinct points in common with the circle `x^2 + y^2 = 9a^2`, then
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Using integration, find the area of the region bounded by the curve y2 = 4x and x2 = 4y.
