Advertisements
Advertisements
प्रश्न
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
उत्तर
`3"x" - 2"y" + 1 = 0 ⇒ "y"_1 =((3"x"+1))/2` ...........(i)
`2"x" - 3"y" - 21 = 0 ⇒ "y"_2 =((21-2"x"))/3` .....(ii)
`"x" - 5"y" + 9 = 0 ⇒ "y"_3 = (("x"+9))/5` ......(iii)
Point of intersection of (i) and (ii) is A(3, 5)
Point of intersection of (ii) and (iii) is B(6, 3) and
Point of intersection of (iii) and (i) is C(1, 2).

Therefore, the area of the region bounded=`int_1^3"y"_1."dx"+int_3^6"y"_2."dx"-int_1^6"y"_3". dx"`
`=int_3^1((3"x"+1))/2."dx"+int_3^6((21-2"x"))/3."dx"-int_1^6(("x"+9))/5."dx"`
`=1/2((3"x"^2)/2+"x")_1^3+1/3(21"x"-"x"^2)_3^6-1/5("x"^2/2+9"x")_1^6`
`1/2[14]+1/3[36]-1/5[125/2]`
`= 7+12-12.5`
`= 6.5 "sq.units"`
APPEARS IN
संबंधित प्रश्न
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Make a rough sketch of the graph of the function y = 4 − x2, 0 ≤ x ≤ 2 and determine the area enclosed by the curve, the x-axis and the lines x = 0 and x = 2.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Find the area of the region bounded by the curve xy − 3x − 2y − 10 = 0, x-axis and the lines x = 3, x = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
The area bounded by y = 2 − x2 and x + y = 0 is _________ .
The ratio of the areas between the curves y = cos x and y = cos 2x and x-axis from x = 0 to x = π/3 is ________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
The area of the circle x2 + y2 = 16 enterior to the parabola y2 = 6x is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.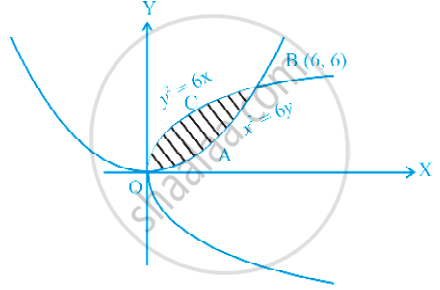
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
Find the area bounded by the curve y = |x – 1| and y = 1, using integration.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
