Advertisements
Advertisements
प्रश्न
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
उत्तर
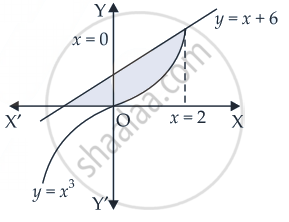
We are given that: y = x3, y = x + 6 and x = 0
Solving y = x3 and y = x + 6
We get x + 6 = x3
⇒ x3 – x – 6 = 0
⇒ x2(x – 2) + 2x(x – 2) + 3(x – 2) = 0
⇒ (x – 2)(x2 + 2x + 3) = 0
x2 + 2x + 3 = 0 has no real roots.
∴ x = 2
∴ Required area of the shaded region
= `int_0^2 (x + 6) "d"x - int_0^2 x^3 "d"x`
= `[x^2/2 + 6x]_0^2 - 1/4 [x^4]_0^2`
= `(4/2 + 12) - (0 + 0) - 1/4 [(2)^4 - 0]`
= `14 - 1/4 xx 16`
= 14 – 4
= 10 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using integration find the area of the region bounded by the curves \[y = \sqrt{4 - x^2}, x^2 + y^2 - 4x = 0\] and the x-axis.
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
Area bounded by parabola y2 = x and straight line 2y = x is _________ .
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
The area bounded by the curve y = f (x), x-axis, and the ordinates x = 1 and x = b is (b −1) sin (3b + 4). Then, f (x) is __________ .
The area bounded by the curve y2 = 8x and x2 = 8y is ___________ .
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Find the area of the region bounded by the curve `y^2 - x` and the line `x` = 1, `x` = 4 and the `x`-axis.
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
Let T be the tangent to the ellipse E: x2 + 4y2 = 5 at the point P(1, 1). If the area of the region bounded by the tangent T, ellipse E, lines x = 1 and x = `sqrt(5)` is `sqrt(5)`α + β + γ `cos^-1(1/sqrt(5))`, then |α + β + γ| is equal to ______.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Find the area of the minor segment of the circle x2 + y2 = 4 cut off by the line x = 1, using integration.
