Advertisements
Advertisements
प्रश्न
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
उत्तर
y = x + 4, if x > 4 and y = -(x+4), if x < 4
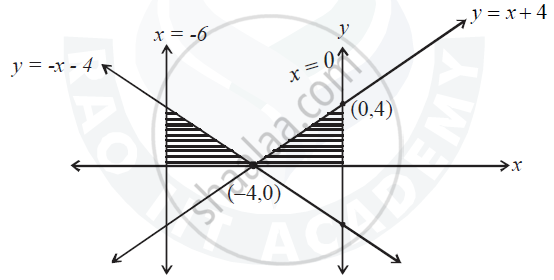
For y = x + 4
when x = 0, y= 4
and when y = 0, x = -4
Point are
∴ (0,4) and (-4,0)
For y = -x - 4
when x = 0, y = -4
when y = 0, x= -4
∴ Point are
(0, -4) and (-4,0)
∴ Required area
`= int_(-6)^(-4)-(x+4) dx + int_(-4)^0 (x + 4) dx`
`= -[x^2/2 + 4x]_(-6)^(-4) + [x^2/2 + 4x]_(-4)^0`
`= [(-4)^2/4 + 4(-4) - [(-6)^2/2 + 4(-6)]] + [0 + 0[(-4)^2/2 + 4(-4)]]`
`= -[16/2 - 16 -[36/2 - 24]] + [-(16/2 - 16)]`
= -[-8 + 6] + [8]
2 + 8 = 10 sq. unit
APPEARS IN
संबंधित प्रश्न
Sketch the graph of y = \[\sqrt{x + 1}\] in [0, 4] and determine the area of the region enclosed by the curve, the x-axis and the lines x = 0, x = 4.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
The area bounded by the curve y = loge x and x-axis and the straight line x = e is ___________ .
The area bounded by the parabola y2 = 4ax, latusrectum and x-axis is ___________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area of the curve y = sin x between 0 and π.
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.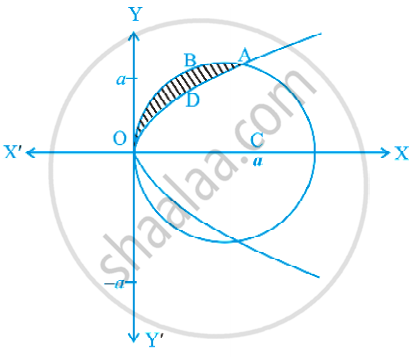
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area of region bounded by the line x = 2 and the parabola y2 = 8x
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis, is
What is the area of the region bounded by the curve `y^2 = 4x` and the line `x` = 3.
Using integration, find the area of the region bounded by the curves x2 + y2 = 4, x = `sqrt(3)`y and x-axis lying in the first quadrant.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
