Advertisements
Advertisements
प्रश्न
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
विकल्प
`4/3`sq.units
1 sq.units
`2/3`sq.units
`1/3`sq.units
उत्तर
The area of the region bounded by parabola y2 = x and the straight line 2y = x is `4/3`sq.units.
Explanation: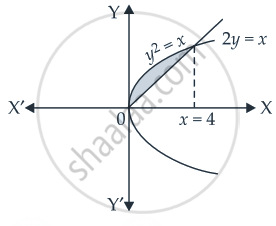
Given equation of parabola is y2 = x ......(i)
And equation of straight line is 2y = x ......(ii)
Solving equation (i) and (ii)
We get `(x/2)^2` = x
⇒ `x^2/4` = x
⇒ x2 = 4x
⇒ x(x – 4) = 0
∴ x = 0, 4
Required area = `int_0^4 sqrt(x) "d"x - int_0^4 x/2 "d"x`
= `2/3 [x^(3/2)]_0^4 - 1/2 * 1/2 [x^2]_0^4`
= `2/3 [(4)^(3/2) - 0] - 1/4 [(4)^2 - 0]`
= `2/3 xx 8 - 1/4 xx 16`
= `16/3 - 4`
= `4/3` sq.units
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 4ax and its latus rectum.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Draw a rough sketch of the graph of the curve \[\frac{x^2}{4} + \frac{y^2}{9} = 1\] and evaluate the area of the region under the curve and above the x-axis.
Draw a rough sketch of the curve \[y = \frac{x}{\pi} + 2 \sin^2 x\] and find the area between the x-axis, the curve and the ordinates x = 0 and x = π.
Find the area bounded by the ellipse \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\] and the ordinates x = ae and x = 0, where b2 = a2 (1 − e2) and e < 1.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region {(x, y) : y2 ≤ 8x, x2 + y2 ≤ 9}.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Find the area of the region included between the parabola y2 = x and the line x + y = 2.
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using integration, find the area of the smaller region bounded by the ellipse `"x"^2/9+"y"^2/4=1`and the line `"x"/3+"y"/2=1.`
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Sketch the region `{(x, 0) : y = sqrt(4 - x^2)}` and x-axis. Find the area of the region using integration.
Using integration, find the area of the region `{(x, y): 0 ≤ y ≤ sqrt(3)x, x^2 + y^2 ≤ 4}`
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Let f(x) be a continuous function such that the area bounded by the curve y = f(x), x-axis and the lines x = 0 and x = a is `a^2/2 + a/2 sin a + pi/2 cos a`, then `f(pi/2)` =
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Let f : [–2, 3] `rightarrow` [0, ∞) be a continuous function such that f(1 – x) = f(x) for all x ∈ [–2, 3]. If R1 is the numerical value of the area of the region bounded by y = f(x), x = –2, x = 3 and the axis of x and R2 = `int_-2^3 xf(x)dx`, then ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Let P(x) be a real polynomial of degree 3 which vanishes at x = –3. Let P(x) have local minima at x = 1, local maxima at x = –1 and `int_-1^1 P(x)dx` = 18, then the sum of all the coefficients of the polynomial P(x) is equal to ______.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
