Advertisements
Advertisements
प्रश्न
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
उत्तर

Points of intersection of two circles is given by solving the equations
\[\left( x - 2 \right)^2 = x^2 \]
\[ \Rightarrow x^2 - 4x + 4 = x^2 \]
\[ \Rightarrow x = 1 \]
\[ \therefore y^2 = 3 \]
\[ \Rightarrow y = \pm \sqrt{3}\]
\[\text{ Now, B}\left( 1, \sqrt{3} \right)\text{ and B'}\left( 1, - \sqrt{3} \right)\text{ are two points of intersection of the two circles }\]
\[\text{ We need to find shaded area }= 2 \times\text{ area }\left(\text{ OBAO }\right) . . . \left( 1 \right)\]
\[\text{ Area }\left(\text{ OBAO }\right) = \text{ area }\left(\text{ OBPO }\right) +\text{ area }\left(\text{ PBAP }\right) \]
\[ = \int_0^1 \left| y_1 \right|dx + \int_1^2 \left| y_2 \right|dx ..............\left\{ \because y_1 > 0 \Rightarrow \left| y_1 \right| = y_1\text{ and }y_2 > 0 \Rightarrow \left| y_2 \right| = y_2 \right\}\]
\[ = \int_0^1 y_1 dx + \int_1^2 y_2 dx\]
\[ = \int_0^1 \sqrt{4 - \left( x - 2 \right)^2} dx + \int_1^2 \sqrt{4 - x^2} dx\]
\[ = \left[ \frac{1}{2}\left( x - 2 \right)\sqrt{4 - \left( x - 2 \right)^2} + \frac{1}{2} \times 4 \times \sin^{- 1} \left( \frac{x - 2}{2} \right) \right]_0^1 + \left[ \frac{1}{2}x\sqrt{4 - x^2} + \frac{1}{2} \times 4 \times \sin^{- 1} \left( \frac{x}{2} \right) \right]_1^2 \]
\[ = \left[ \frac{- \sqrt{3}}{2} + 2 \sin^{- 1} \left( \frac{- 1}{2} \right) \right] - \left[ 0 + 2 \sin^{- 1} \left( - 1 \right) \right] + \left( 0 - \frac{1}{2}\sqrt{3} \right) + 2\left\{ si n^{- 1} \left( 1 \right) - si n^{- 1} \left( \frac{1}{2} \right) \right\}\]
\[ = \frac{- \sqrt{3}}{2} + 2 \sin^{- 1} \left( \frac{- 1}{2} \right) - 0 - 2 \sin^{- 1} \left( - 1 \right) + 0 - \frac{1}{2}\sqrt{3} + 2si n^{- 1} \left( 1 \right) - 2si n^{- 1} \left( \frac{1}{2} \right)\]
\[ = - \sqrt{3} - 4 \sin^{- 1} \left( \frac{1}{2} \right) + 4 \sin^{- 1} \left( 1 \right)\]
\[ = - \sqrt{3} - 4 \times \frac{\pi}{6} + 4 \times \frac{\pi}{2}\]
\[ = - \sqrt{3} - \frac{2\pi}{3} + 2\pi\]
\[ = \frac{4\pi}{3} - \sqrt{3}\]
\[\text{ Now, From equation }\left( 1 \right)\]
\[\text{ Shaded area }= 2 \times\text{ area }\left(\text{ OBAO }\right) = 2\left( \frac{4\pi}{3} - \sqrt{3} \right) = \left( \frac{8\pi}{3} - 2\sqrt{3} \right)\text{ sq units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area bounded by the curve y = cos x, x-axis and the ordinates x = 0 and x = 2π.
Calculate the area of the region bounded by the parabolas y2 = x and x2 = y.
Find the area of the region bounded by y =\[\sqrt{x}\] and y = x.
Draw a rough sketch and find the area of the region bounded by the two parabolas y2 = 4x and x2 = 4y by using methods of integration.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area bounded by the parabola y = 2 − x2 and the straight line y + x = 0.
Find the area of the region enclosed between the two curves x2 + y2 = 9 and (x − 3)2 + y2 = 9.
Find the area enclosed by the curves y = | x − 1 | and y = −| x − 1 | + 1.
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
The area bounded by the parabola x = 4 − y2 and y-axis, in square units, is ____________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
The area bounded by the curve y = x |x| and the ordinates x = −1 and x = 1 is given by
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.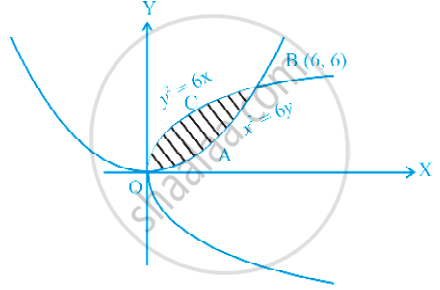
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
Area (in sq.units) of the region outside `|x|/2 + |y|/3` = 1 and inside the ellipse `x^2/4 + y^2/9` = 1 is ______.
Area of figure bounded by straight lines x = 0, x = 2 and the curves y = 2x, y = 2x – x2 is ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
Let g(x) = cosx2, f(x) = `sqrt(x)`, and α, β (α < β) be the roots of the quadratic equation 18x2 – 9πx + π2 = 0. Then the area (in sq. units) bounded by the curve y = (gof)(x) and the lines x = α, x = β and y = 0, is ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Sketch the region bounded by the lines 2x + y = 8, y = 2, y = 4 and the Y-axis. Hence, obtain its area using integration.
Find the area of the following region using integration ((x, y) : y2 ≤ 2x and y ≥ x – 4).
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
Using integration, find the area bounded by the curve y2 = 4ax and the line x = a.
