Advertisements
Advertisements
प्रश्न
Area of the region bounded by the curve y = cosx between x = 0 and x = π is ______.
विकल्प
2 sq.units
4 sq.units
3 sq.units
1 sq.units
उत्तर
Area of the region bounded by the curve y = cosx between x = 0 and x = π is 2 sq.units.
Explanation:
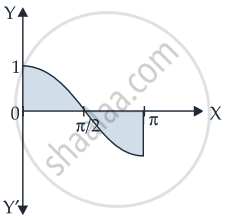
Given that: y = cos x, x = 0, x = π
Required area = `int_0^(pi/2) cos x "d"x + |int_(pi/2)^pi cos x "d"x|`
= `[sin x]_0^(pi/2) + |(sin x)_(pi/2)^pi|`
= `[sin pi/2 - sin 0] + |[sin pi - sin pi/2]|`
= `(1 - 0) + |0 - 1|`
= 1 + 1
= 2 sq.units
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y2 = 4ax, x-axis and the lines x = 0 and x = a.
Find the area of the region common to the circle x2 + y2 =9 and the parabola y2 =8x
Sketch the region bounded by the curves `y=sqrt(5-x^2)` and y=|x-1| and find its area using integration.
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Draw a rough sketch to indicate the region bounded between the curve y2 = 4x and the line x = 3. Also, find the area of this region.
Draw a rough sketch of the curve y = \[\frac{\pi}{2} + 2 \sin^2 x\] and find the area between x-axis, the curve and the ordinates x = 0, x = π.
Find the area of the minor segment of the circle \[x^2 + y^2 = a^2\] cut off by the line \[x = \frac{a}{2}\]
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
Find the area of the region between the circles x2 + y2 = 4 and (x − 2)2 + y2 = 4.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area of the region {(x, y): x2 + y2 ≤ 4, x + y ≥ 2}.
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
Area lying in first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2, is
Using integration, find the area of the region bounded by the line x – y + 2 = 0, the curve x = \[\sqrt{y}\] and y-axis.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area enclosed by the curve y = –x2 and the straight lilne x + y + 2 = 0
Find the area bounded by the curve y = 2cosx and the x-axis from x = 0 to x = 2π
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
The curve x = t2 + t + 1,y = t2 – t + 1 represents
Find the area of the region bounded by the ellipse `x^2/4 + y^2/9` = 1.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Let f(x) be a non-negative continuous function such that the area bounded by the curve y = f(x), x-axis and the ordinates x = `π/4` and x = `β > π/4` is `(βsinβ + π/4 cos β + sqrt(2)β)`. Then `f(π/2)` is ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
