Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the triangle ABC whose vertices A, B, C are (−1, 1), (0, 5) and (3, 2) respectively.
उत्तर
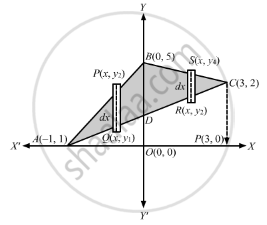
Equation of line AB is
\[y - 1 = \left( \frac{5 - 1}{0 + 1} \right)\left( x - \left( - 1 \right) \right)\]
\[ \Rightarrow y = 4x + 5 \]
Area under the line AB = area ABDO
\[ = \int_{- 1}^0 \left( 4x + 5 \right) dx\]
\[ = \left[ 4\frac{x^2}{2} + 5x \right]_{- 1}^0 \]
\[ = 0 - \left( 2 - 5 \right)\]
\[ \Rightarrow\text{ Area ABDO }= 3\text{ sq . units .} . . \left( 1 \right)\]
Equation of line BC is
\[y - 5 = \left( \frac{2 - 5}{3 - 0} \right)\left( x - 0 \right)\]
\[ \Rightarrow y = - x + 5\]
Area under line BC = Area OBCP
\[ = \int_0^3 \left( - x + 5 \right) dx\]
\[ = \left[ - \frac{x^2}{2} + 5x \right]_0^3 \]
\[ = - \frac{9}{2} + 15 - 0\]
\[ \Rightarrow\text{ Area OBCP }= \frac{21}{2}\text{ sq . units . }. . \left( 2 \right)\]
Equation of line CA is
\[y - 2 = \left( \frac{2 - 1}{3 - \left( - 1 \right)} \right)\left( x - 3 \right) \]
\[ \Rightarrow 4y = x + 5\]
\[ \therefore\text{ Area under line AC = Area ACPA }\]
\[ \Rightarrow A = \int_{- 1}^3 \left( \frac{x + 5}{4} \right)dx\]
\[ \Rightarrow A = \frac{1}{4} \left[ \frac{x}{2}^2 + 5x \right]_{- 1}^3 \]
\[ \Rightarrow A = \frac{1}{4}\left[ \frac{3}{2}^2 + 5 \times 3 - \frac{\left( - 1 \right)}{2}^2 + 5\left( - 1 \right) \right]\]
\[ \Rightarrow A = \frac{1}{4}\left[ \frac{9}{2} + 15 - \frac{1}{2} + 5 \right]\]
\[ \Rightarrow\text{ Area ACPA }= \frac{24}{4} = 6 \text{ sq . units }. . . \left( 3 \right)\]
\[\text{ From }\left( 1 \right), \left( 2 \right)\text{ and }\left( 3 \right)\]
\[\text{ Area }\Delta\text{ ABC }=\text{ Area ABDO + Area OBCP - Area ACPA }\]
\[ \Rightarrow A = 3 + \frac{21}{2} - 6\]
\[ \Rightarrow A = \frac{21}{2} - 3 = \frac{21 - 6}{2} = \frac{15}{2} \text{ sq . units }\]
\[ \therefore\text{ Area }\Delta\text{ ABC }= \frac{15}{2}\text{ sq . units }\]
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the curve x2 = 16y, lines y = 2, y = 6 and Y-axis lying in the first quadrant.
Sketch the graph of y = |x + 4|. Using integration, find the area of the region bounded by the curve y = |x + 4| and x = –6 and x = 0.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Using integration, find the area of the region bounded by the triangle whose vertices are (2, 1), (3, 4) and (5, 2).
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area enclosed by the parabolas y = 5x2 and y = 2x2 + 9.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area enclosed by the curve \[y = - x^2\] and the straight line x + y + 2 = 0.
Using the method of integration, find the area of the region bounded by the following lines:
3x − y − 3 = 0, 2x + y − 12 = 0, x − 2y − 1 = 0.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area bounded by the parabola x = 8 + 2y − y2; the y-axis and the lines y = −1 and y = 3.
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using horizontal strips.
If An be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4, then for x > 2
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
Find the area of the region bound by the curves y = 6x – x2 and y = x2 – 2x
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
The area enclosed by the circle x2 + y2 = 2 is equal to ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2
Draw a rough sketch of the region {(x, y) : y2 ≤ 6ax and x 2 + y2 ≤ 16a2}. Also find the area of the region sketched using method of integration.
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is ______.
Using integration, find the area of the region in the first quadrant enclosed by the line x + y = 2, the parabola y2 = x and the x-axis.
The region bounded by the curves `x = 1/2, x = 2, y = log x` and `y = 2^x`, then the area of this region, is
Find the area of the region bounded by the curve `y = x^2 + 2, y = x, x = 0` and `x = 3`
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
