Advertisements
Advertisements
प्रश्न
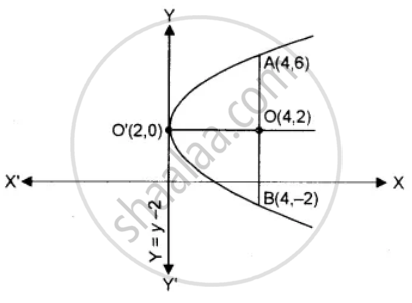
Find the equation of the parabola with latus-rectum joining points (4, 6) and (4, -2).
उत्तर
Joining points are (4, 6) and (4, -2)
Length of latus - rectum = 4a
∴ `sqrt((4 - 4)^2 + (6+ 2)^2) = 4a`
⇒ `sqrt((8)^2)` = 4a
∴ 4a = 8
Hence, equation of parabola
Y2 = 4ax
Y2 = 8x
∴ (y -2)2 = 8x
APPEARS IN
संबंधित प्रश्न
Prove that the curves y2 = 4x and x2 = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Find the area of ellipse `x^2/1 + y^2/4 = 1`
Find the area lying above the x-axis and under the parabola y = 4x − x2.
Find the area of the region bounded by x2 = 4ay and its latusrectum.
Prove that the area in the first quadrant enclosed by the x-axis, the line x = \[\sqrt{3}y\] and the circle x2 + y2 = 4 is π/3.
Find the area common to the circle x2 + y2 = 16 a2 and the parabola y2 = 6 ax.
OR
Find the area of the region {(x, y) : y2 ≤ 6ax} and {(x, y) : x2 + y2 ≤ 16a2}.
Find the area of the region enclosed by the parabola x2 = y and the line y = x + 2.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x − x2 and y = x2− x?
Find the area of the region between the parabola x = 4y − y2 and the line x = 2y − 3.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x − y = 4.
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area of the region bounded by the parabola y = x2 + 1 and the straight line x + y = 3 is given by
Area bounded by the curve y = x3, the x-axis and the ordinates x = −2 and x = 1 is ______.
Find the area of the region bounded by the curve ay2 = x3, the y-axis and the lines y = a and y = 2a.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.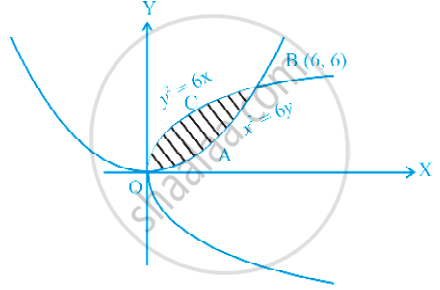
Find the area of the region bounded by y = `sqrt(x)` and y = x.
Find the area of region bounded by the triangle whose vertices are (–1, 1), (0, 5) and (3, 2), using integration.
The area of the region bounded by the curve y = `sqrt(16 - x^2)` and x-axis is ______.
The area of the region bounded by parabola y2 = x and the straight line 2y = x is ______.
The area of the region bounded by the circle x2 + y2 = 1 is ______.
Using integration, find the area of the region bounded between the line x = 4 and the parabola y2 = 16x.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area of the region enclosed by the curves y2 = x, x = `1/4`, y = 0 and x = 1, using integration.
The area (in sq.units) of the region A = {(x, y) ∈ R × R/0 ≤ x ≤ 3, 0 ≤ y ≤ 4, y ≤x2 + 3x} is ______.
The area of the region bounded by the parabola (y – 2)2 = (x – 1), the tangent to it at the point whose ordinate is 3 and the x-axis is ______.
