Advertisements
Advertisements
प्रश्न
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
विकल्प
- \[\frac{16}{3}\]
- \[\frac{23}{3}\]
- \[\frac{32}{3}\]
- \[\frac{16\sqrt{2}}{3}\]
उत्तर
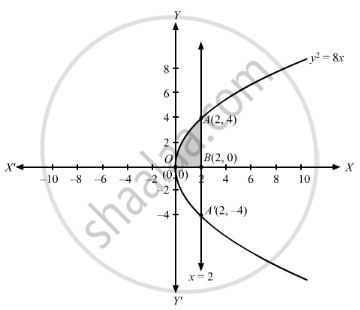
y2 = 8x represents a parabola opening side ways , with vertex at O(0, 0) and Focus at B(2, 0)
Thus AA' represents the latus rectum of the parabola.
The points of intersection of the parabola and latus rectum are A(2, 4) and A'(2, −4)
Area bound by curve , x-axis and latus rectum is the area OABO,
\[\text{ The approximating rectangle of width = dx and length }= \left| y \right| \text{ has area }= \left| y \right| dx,\text{ and moves from }x = 0\text{ to }x = 2\]
\[\text{ area }\left( OABO \right) = \int_0^2 \left| y \right| dx\]
\[ = \int_0^2 y dx ............\left\{ y > 0 , \Rightarrow \left| y \right| = y \right\}\]
\[ = \int_0^2 \sqrt{8x}dx\]
\[ = 2\sqrt{2} \int_0^2 \sqrt{x}dx\]
\[ = 2\sqrt{2} \left[ \frac{x^\frac{3}{2}}{\frac{3}{2}} \right]_0^2 \]
\[ = 2\sqrt{2} \times \frac{2}{3}\left( 2^\frac{3}{2} - 0 \right)\]
\[ = 4\frac{\sqrt{2}}{3} \times 2\sqrt{2}\]
\[ = \frac{16}{3} \text{ sq units }\]
APPEARS IN
संबंधित प्रश्न
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is ______.
Using integration, find the area of the region bounded between the line x = 2 and the parabola y2 = 8x.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Find the area of the region bounded by x2 + 16y = 0 and its latusrectum.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Find the area, lying above x-axis and included between the circle x2 + y2 = 8x and the parabola y2 = 4x.
Find the area of the region in the first quadrant enclosed by x-axis, the line y = \[\sqrt{3}x\] and the circle x2 + y2 = 16.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Find the area bounded by the curves x = y2 and x = 3 − 2y2.
Find the area of the circle x2 + y2 = 16 which is exterior to the parabola y2 = 6x.
Find the area of the region bounded by the curve y = \[\sqrt{1 - x^2}\], line y = x and the positive x-axis.
Using integration, find the area of the following region: \[\left\{ \left( x, y \right) : \frac{x^2}{9} + \frac{y^2}{4} \leq 1 \leq \frac{x}{3} + \frac{y}{2} \right\}\]
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area bounded by the curve y = x4 − 2x3 + x2 + 3 with x-axis and ordinates corresponding to the minima of y is _________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The closed area made by the parabola y = 2x2 and y = x2 + 4 is __________ .
The area of the region (in square units) bounded by the curve x2 = 4y, line x = 2 and x-axis is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Using integration, find the area of the region bounded by the parabola y2 = 4x and the circle 4x2 + 4y2 = 9.
Using the method of integration, find the area of the region bounded by the lines 3x − 2y + 1 = 0, 2x + 3y − 21 = 0 and x − 5y + 9 = 0
Find the area of the curve y = sin x between 0 and π.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.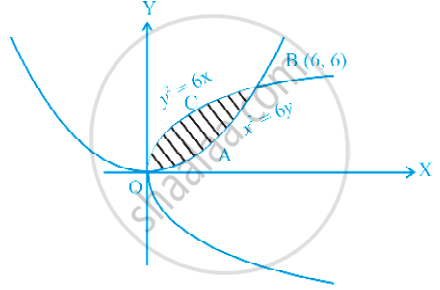
The area of the region bounded by the curve y = x2 + x, x-axis and the line x = 2 and x = 5 is equal to ______.
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the line y = 4 and the curve y = x2 is ______.
Area lying in the first quadrant and bounded by the circle `x^2 + y^2 = 4` and the lines `x + 0` and `x = 2`.
Find the area of the region bounded by curve 4x2 = y and the line y = 8x + 12, using integration.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Let a and b respectively be the points of local maximum and local minimum of the function f(x) = 2x3 – 3x2 – 12x. If A is the total area of the region bounded by y = f(x), the x-axis and the lines x = a and x = b, then 4A is equal to ______.
The area (in square units) of the region bounded by the curves y + 2x2 = 0 and y + 3x2 = 1, is equal to ______.
Using integration, find the area of the region bounded by y = mx (m > 0), x = 1, x = 2 and the X-axis.
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
