Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
Advertisements
उत्तर
The equations of the given lines are
y = 2 + x .....(1)
y = 2 – x .....(2)
x = 2 .....(3)
Solving (1), (2) and (3) in pairs, we obtain the coordinates of the point of intersection as A(0, 2), B(2, 4) and C(2, 0).
The graphs of these lines are drawn as shown in the figure below.
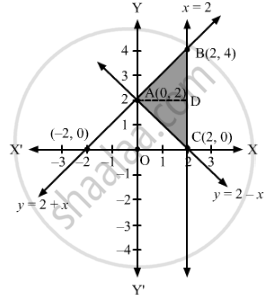
Here, the shaded region represents the area bounded by the given lines.
∴ Required area = Area of the region ABCA
= Area of region ACDA + Area of region ABDA
`=∫_0^2xAC dy+∫_2^4xAB dy`
`=∫_0^2(2−y)dy+∫_2^4(y−2)dy`
`=(2y-y^2/2)_0^2+(Y^2/2-2y)_2^4`
=[(4−2)−(0−0)]+[(8−8)−(2−4)]
=2+2
=4 square units
Thus, the area of the region bounded by the given lines is 4 square units.
APPEARS IN
संबंधित प्रश्न
Find the area of the region bounded by the parabola y2 = 16x and the line x = 3.
Using integration, find the area of the region bounded by the line y − 1 = x, the x − axis and the ordinates x= −2 and x = 3.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Show that the areas under the curves y = sin x and y = sin 2x between x = 0 and x =\[\frac{\pi}{3}\] are in the ratio 2 : 3.
Draw a rough sketch of the region {(x, y) : y2 ≤ 5x, 5x2 + 5y2 ≤ 36} and find the area enclosed by the region using method of integration.
Sketch the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 1. Also, find the area of this region.
Find the area enclosed by the curves 3x2 + 5y = 32 and y = | x − 2 |.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
Find the area of the figure bounded by the curves y = | x − 1 | and y = 3 −| x |.
The area of the region bounded by the parabola (y − 2)2 = x − 1, the tangent to it at the point with the ordinate 3 and the x-axis is _________ .
The area of the region \[\left\{ \left( x, y \right) : x^2 + y^2 \leq 1 \leq x + y \right\}\] is __________ .
The area bounded by the parabola y2 = 8x, the x-axis and the latusrectum is ___________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Sketch the graphs of the curves y2 = x and y2 = 4 – 3x and find the area enclosed between them.
Find the area of the region bounded by the parabola y2 = 2x and the straight line x – y = 4.
The area enclosed by the ellipse `x^2/"a"^2 + y^2/"b"^2` = 1 is equal to ______.
Find the area of the region bounded by the curve y = x3 and y = x + 6 and x = 0
Find the area of the region bounded by the curve y2 = 4x, x2 = 4y.
Find the area bounded by the curve y = `sqrt(x)`, x = 2y + 3 in the first quadrant and x-axis.
The area of the region bounded by the curve x2 = 4y and the straight line x = 4y – 2 is ______.
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2 = 32 is ______.
The area of the region bounded by the curve y = sinx between the ordinates x = 0, x = `pi/2` and the x-axis is ______.
The area of the region bounded by the ellipse `x^2/25 + y^2/16` = 1 is ______.
Area of the region bounded by the curve y = |x + 1| + 1, x = –3, x = 3 and y = 0 is
The area bounded by `y`-axis, `y = cosx` and `y = sinx, 0 ≤ x - (<pi)/2` is
For real number a, b (a > b > 0),
let Area `{(x, y): x^2 + y^2 ≤ a^2 and x^2/a^2 + y^2/b^2 ≥ 1}` = 30π
Area `{(x, y): x^2 + y^2 ≥ b^2 and x^2/a^2 + y^2/b^2 ≤ 1}` = 18π.
Then the value of (a – b)2 is equal to ______.
The area of the region S = {(x, y): 3x2 ≤ 4y ≤ 6x + 24} is ______.
Find the area of the smaller region bounded by the curves `x^2/25 + y^2/16` = 1 and `x/5 + y/4` = 1, using integration.
Sketch the region enclosed bounded by the curve, y = x |x| and the ordinates x = −1 and x = 1.
Evaluate:
`int_0^1x^2dx`
