Advertisements
Advertisements
प्रश्न
Using integration, find the area of the region bounded by the lines y = 2 + x, y = 2 – x and x = 2.
उत्तर
The equations of the given lines are
y = 2 + x .....(1)
y = 2 – x .....(2)
x = 2 .....(3)
Solving (1), (2) and (3) in pairs, we obtain the coordinates of the point of intersection as A(0, 2), B(2, 4) and C(2, 0).
The graphs of these lines are drawn as shown in the figure below.
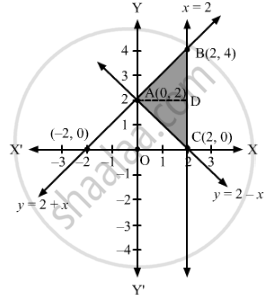
Here, the shaded region represents the area bounded by the given lines.
∴ Required area = Area of the region ABCA
= Area of region ACDA + Area of region ABDA
`=∫_0^2xAC dy+∫_2^4xAB dy`
`=∫_0^2(2−y)dy+∫_2^4(y−2)dy`
`=(2y-y^2/2)_0^2+(Y^2/2-2y)_2^4`
=[(4−2)−(0−0)]+[(8−8)−(2−4)]
=2+2
=4 square units
Thus, the area of the region bounded by the given lines is 4 square units.
APPEARS IN
संबंधित प्रश्न
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5.
Find the area of the region bounded by the parabola y2 = 4ax and the line x = a.
Find the area under the curve y = \[\sqrt{6x + 4}\] above x-axis from x = 0 to x = 2. Draw a sketch of curve also.
Determine the area under the curve y = \[\sqrt{a^2 - x^2}\] included between the lines x = 0 and x = a.
Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8.
Using definite integrals, find the area of the circle x2 + y2 = a2.
Using integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + | x + 1 |, x = −2, x = 3, y = 0.
Sketch the graph y = | x + 1 |. Evaluate\[\int\limits_{- 4}^2 \left| x + 1 \right| dx\]. What does the value of this integral represent on the graph?
Find the area of the region bounded by x2 = 16y, y = 1, y = 4 and the y-axis in the first quadrant.
Find the area bounded by the curve y = 4 − x2 and the lines y = 0, y = 3.
Draw a rough sketch of the region {(x, y) : y2 ≤ 3x, 3x2 + 3y2 ≤ 16} and find the area enclosed by the region using method of integration.
Find the area of the region bounded by \[y = \sqrt{x}, x = 2y + 3\] in the first quadrant and x-axis.
Find the area of the region bounded by \[y = \sqrt{x}\] and y = x.
Find the area of the region bounded by the curves y = x − 1 and (y − 1)2 = 4 (x + 1).
Using integration find the area of the region:
\[\left\{ \left( x, y \right) : \left| x - 1 \right| \leq y \leq \sqrt{5 - x^2} \right\}\]
Find the area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle x2 + y2= 32.
Find the area bounded by the lines y = 4x + 5, y = 5 − x and 4y = x + 5.
Find the area enclosed by the parabolas y = 4x − x2 and y = x2 − x.
The area bounded by the curve y = 4x − x2 and the x-axis is __________ .
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
Find the area bounded by the parabola y2 = 4x and the line y = 2x − 4 By using vertical strips.
Find the area of the region bounded by the parabolas y2 = 6x and x2 = 6y.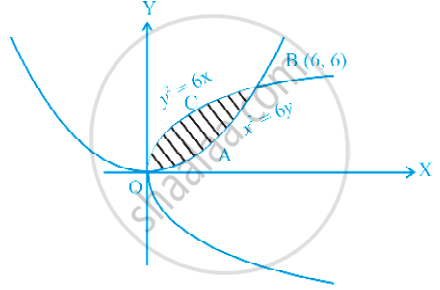
Find the area of the region above the x-axis, included between the parabola y2 = ax and the circle x2 + y2 = 2ax.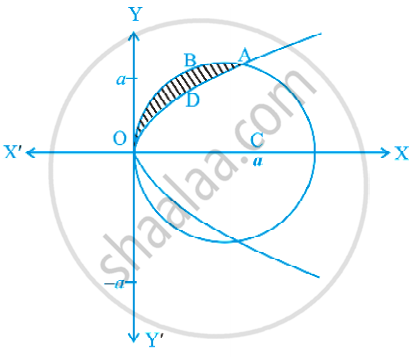
Find the area of the region bounded by the parabola y2 = 2px, x2 = 2py
Find the area of the region included between y2 = 9x and y = x
Draw a rough sketch of the given curve y = 1 + |x +1|, x = –3, x = 3, y = 0 and find the area of the region bounded by them, using integration.
Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.
The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1
Find the area of the region bounded by the curve x2 = 4y and the line x = 4y – 2.
Hence find the area bounded by the curve, y = x |x| and the coordinates x = −1 and x = 1.
